高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | |||
| 5. 置換積分法(定積分) | |||
| 6. 部分積分法(定積分) | |||
| 7. 定積分と微分法 | |||
| 8. 定積分と和の極限 | |||
| 9. 定積分と不等式 | |||
| 10. 定積分の応用(面積) | |||
| 11. 定積分の応用(体積) | |||
| 12. 定積分の応用(回転体の体積) | |||
| 13. 曲線の長さ |

12.定積分の応用(回転体の体積)
12.1 回転体の体積
回転体では切り方がいつも決まっている
立体の体積を積分で求めるには,ある方向に切り口を定め,その切り口における断面積を求めて,あとはその断面と垂直な方向に積分すればよかった(定積分の応用(体積) 参照).
このとき難しいのは,どういった切り口を考えるかであって,切り方によっては計算の難易度が劇的に変化する場合も多い.非回転体の求積が難問化しやすい訳はここにある.
それに対して回転体の求積はそういった試行錯誤が必要ない.
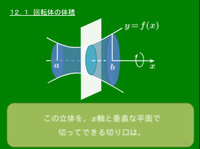
いつも切る方向は決まっていて,回転軸に対して垂直な平面で切断するのが定石である.
何故ならこのような切り方で現れる切り口はいつでも円形かドーナツ型をしているので,断面積の計算がとてもやさしくなるからだ.
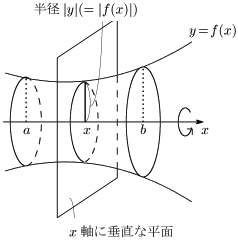
曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=a$,$x=b$ $(a < b)$ で囲まれた部分を $x$ 軸のまわりに1回転させてできる回転体の体積を $V$ とする.
この立体を $x$ 軸と垂直な平面で切ってできる切り口は,半径 $|y|\ (=|f(x)|)$ の円であるから,切り口の面積は,
\[\pi y^2\ (=\pi\{f(x)\}^2)\]
である.従って,次が成り立つ:
回転体の体積
\[V=\pi\int_a^b\!\!y^2\,dx=\pi\int_a^b\!\!\{f(x)\}^2\,dx\]
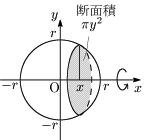
例題 半径 $r$ の球の体積 $V$ を求めよ.
こたえ

12.2 2曲線の間の領域の回転体
2曲線が $x$ 軸の片側にあるとき,切り口はドーナツ型
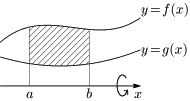
関数 $f(x),\ g(x)$ が区間 $[a,b]$ で常に $f(x)\geqq g(x)\geqq0$ であるとする.
このとき,2曲線 $y=f(x),\ y=g(x)$,及び 2直線 $x=a,\ x=b$ で囲まれた部分を $x$ 軸のまわりに1回転して得られる回転体の体積 $V$ は,次で求められる.
\[\begin{align*}
V&=\pi\int_a^b\!\!\{f(x)\}^2\,dx-\pi\int_a^b\!\!\{g(x)\}^2\,dx\\[5pt]
&=\pi\int_a^b\!\!(f^2-g^2)\,dx\\[5pt]
& (f,\,g\ \mbox{のあとの「} \,(x)\, \mbox{」を省略した.})
\end{align*}\]
2曲線で囲まれる回転体の体積
\[V=\pi\int_a^b\!\!(f^2-g^2)\,dx\]
注意
$V=\pi\displaystyle\int_a^b\!\!(f-g)^2\,dx$ ではない!!
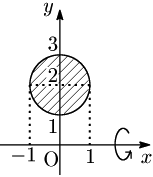
こたえ
$x^2+(y-2)^2=1$ を $y$ について解くと,
\[y=\left\{\begin{array}{ll}
2+\sqrt{1-x^2}&(\mbox{円の上半分})\ \cdots\mbox{①}\\[5pt]
2-\sqrt{1-x^2}&(\mbox{円の下半分})\ \cdots\mbox{②}
\end{array}\right.\]
①$\geqq$②$\geqq 0$ であるから,
\[\begin{align*}
V&=\pi\int_{-1}^1\!\!\left(\mbox{①}^2-\mbox{②}^2\right)\,dx\\[5pt]
&=8\pi\int_{-1}^1\!\!\sqrt{1-x^2}\,dx\\[5pt]
&=8\pi\times\frac\pi2\\[5pt]
&=\underline{\boldsymbol{4\pi^2}}
\end{align*}\]

補足
$\displaystyle\int_{-1}^1\!\sqrt{1-x^2}\,dx=\frac\pi2$ の部分は積分を実行するのではなく,直ちに $\dfrac\pi2$ と答えたい.詳しくは こちら を参照.

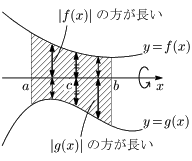
12.3 領域が回転軸をまたぐ場合
回転軸をまたぐ場合は長い方が強い