高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | |||
| 5. 置換積分法(定積分) | |||
| 6. 部分積分法(定積分) | |||
| 7. 定積分と微分法 | |||
| 8. 定積分と和の極限 | |||
| 9. 定積分と不等式 | |||
| 10. 定積分の応用(面積) | |||
| 11. 定積分の応用(体積) | |||
| 12. 定積分の応用(回転体の体積) | |||
| 13. 曲線の長さ |

8.定積分と和の極限
8.1 区分求積法
まずは簡単な例から
例として,放物線 $y=x^2$,2直線 $x=-1,\ x=2$ 及び $x$ 軸で囲まれた部分の面積 $S$ を求めることを考えよう.
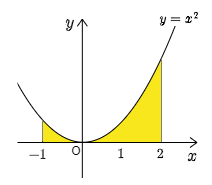
黄色い部分の面積が $S$ であり,
\[S=\int_{-1}^2x^2\,dx\]
で求められる.実際に計算すると $S=3$ である.
次にこの面積を別の視点から眺めてみよう.
まず,$-1$ から $2$ までを6等分して,図のように6つの長方形の面積の総和で近似してみる.
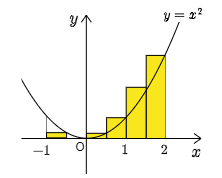
各長方形の横の長さはどれも $\dfrac12$ である.一方,縦の長さは $y=x^2$ によって左から順に計算すると
\[\left(-\dfrac12\right)^2,\ 0^2,\ \left(\dfrac12\right)^2,\ 1^2,\ \left(\dfrac32\right)^2,\ 2^2\]
となるから,長方形の面積はそれぞれ
\[\dfrac18,\ 0,\ \dfrac18,\ \dfrac12,\ \dfrac98,\ 2\]
となる.よって
\[\begin{align*}
S&\fallingdotseq\dfrac18+0+\dfrac18+\dfrac12+\dfrac98+2\\[5pt]
&=\dfrac{31}8\\[5pt]
&=3.875
\end{align*}\]
となる.荒っぽい近似であったせいか,さすがにこれでは精度が悪い.
もう少しマシな近似を試みる
では長方形の横の長さを,さっきの半分である $\dfrac14$ にしてみるとどうだろう.つまり,$-1$ から $2$ までを12等分するのだ.
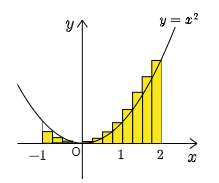
長方形は細分され,縦の長さは左から順に
\[\dfrac9{16},\ \dfrac4{16},\ \dfrac1{16},\ 0,\ \dfrac1{16},\ \dfrac4{16},\ \dfrac9{16},\ 1,\ \dfrac{25}{16},\ \dfrac{36}{16},\ \dfrac{49}{16},\ 4\]
となるから,長方形の面積はそれぞれ
\[\dfrac9{64},\ \dfrac4{64},\ \dfrac1{64},\ 0,\ \dfrac1{64},\ \dfrac4{64},\ \dfrac9{64},\ \dfrac14,\ \dfrac{25}{64},\ \dfrac{36}{64},\ \dfrac{49}{64},\ 1\]
となる.これらの面積の総和を計算すると
\[\begin{align*}
S&\fallingdotseq \dfrac14+\dfrac9{64}+\dfrac4{64}+\dfrac1{64}+0+\dfrac1{64}+\dfrac4{64}\\[5pt]
&\hspace{5mm}+\dfrac9{64}+\dfrac14+\dfrac{25}{64}+\dfrac{36}{64}+\dfrac{49}{64}\\[5pt]
&=\dfrac{218}{64}\\[5pt]
&\fallingdotseq 3.406
\end{align*}\]
となり,さっきよりは3に近付いた.誤差が小さくなったというのは上の図からも納得できるであろう.
表現を簡潔にしておく
ところですぐ上の式は,12個の数を足すために式が長くなり,大変読みにくくなってしまった.これをもっと見やすくするには和の記号 $\displaystyle\sum$ を用いればよい.
$f(x)=x^2$,$x_k=-1+\dfrac14k$ とおくと,左から $k$ 番目の長方形は,高さが $f(x_k)$ だから,面積は $\dfrac14f(x_k)$ と表せる.よって
\[S\fallingdotseq\dfrac14\sum_{k=1}^{12} f(x_k)\]
というようにスッキリと書ける.
これは実に見やすいし,意味も取りやすい.
より良い近似を求めて
さて,このようにして分割の幅を小さくしていくと,縦に細長い長方形の面積の総和と $S$ との差はどんどん小さくなる.
分割の幅を小さくするというのは換言すれば,分割の個数 $n$ を大きくすることである.$n\to\infty$ の極限を考えると,$S$ との誤差が限りなく0に近づき,
$\displaystyle S=\lim_{n\to\infty}($長方形の面積の総和$)$
というように,「$\fallingdotseq$」から「$=$」になることが期待される.
これを式で表すと,分割の個数が $n$ のとき,1つ1つの長方形の横の長さが $\dfrac{2-(-1)}n=\dfrac3n$ となるから,$x_k=-1+\dfrac 3nk$ として
\[S=\lim_{n\to\infty}\sum_{k=1}^n \dfrac 3n f(x_k)\]
である.
$S$ は元々 $\displaystyle\int_{-1}^2 x^2\,dx$ であったから,次が成り立つ.
\[\int_{-1}^2 x^2\,dx=\lim_{n\to\infty}\sum_{k=1}^n \dfrac 3n f(x_k)\]
高校数学においては,右辺のような式が現れたときに,左辺の積分に持ち込んで計算するという使われ方が一般的である.つまり上の式の両辺を入れ替えて,$f(x_k)$ を具体的に書くと
\[\lim_{n\to\infty}\sum_{k=1}^n \dfrac 3n \left(1+\dfrac 3n k\right)^2dx=\int_{-1}^2 x^2\,dx\]
という風にして,左辺の式の値を求めるのに,右辺の積分を計算するといった具合である.
理論的にはこれでよいのであるが,実用上は,下の補足2にあるように,積分区間を $[0,\ 1]$ にして計算するのがやりやすい.詳しくは「8.2 いくつかの例題」を参照.

それでは一般論
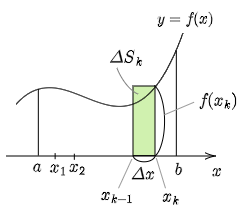
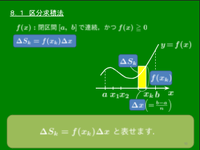
一般に,関数 $f(x)$ は区間 $[a,b]$ で連続,かつ $f(x)\geqq 0$ とする.この区間を $n$ 等分して,その分点を順に
\[x_0(=a),\ x_1,\ x_2,\ \cdots ,\ x_n(=b)\]
とおき,各区間の幅を $\Delta x\left(=\dfrac{b-a}n\right)$ とおく.曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=x_{k-1}$,$x=x_k$ $(k=1,2,\cdots,n)$ とで囲まれる部分の面積は,次の長方形領域(図の緑色)の面積 $\Delta S_k$ で近似される:
\[\Delta S_k=f(x_k)\Delta x\]
よって曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=a$,$x=b$ で囲まれる部分の面積 $S$ は,次の①式で近似される.
$\displaystyle S\fallingdotseq\sum_{k=1}^n\Delta S_k=\sum_{k=1}^nf(x_k)\Delta x\ \ \cdots$ ①
ここで $n$ を $n\to\infty$ として分割をどんどん細かくしていくと,①で $S$ を近似したときの誤差は限りなく0に近付くであろう.即ち \[S=\lim_{n\to\infty}\sum_{k=1}^nf(x_k)\Delta x\] となる.$S=\displaystyle\int_a^b\!\!f(x)\,dx$ であったから次が成り立つ:
定積分と和の極限\[ \lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x=\int_a^b\!\!f(x)dx \]
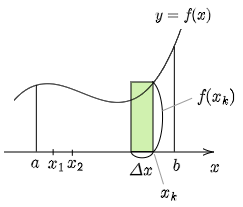
左辺の $f(x_k)$ と $\Delta x$ の順序を交換して,式を具体的に書き下した表現にすると次のようになる.
\[\lim_{n\to\infty} \sum_{k=1}^n \dfrac{b-a}n f\left(a+\dfrac{b-a}nk\right)=\int_a^b\!\!f(x)\,dx \]
このように,対象となる領域の面積を微細な長方形の和の極限として求める方法を区分求積法という.
補足1
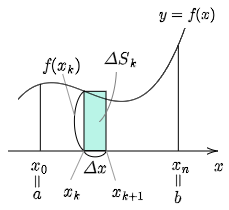
上の囲みの式を,和をとる番号を $k=0$ から $n-1$ の $n$ 個にして, \[\lim_{n\to\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_a^b\!\!f(x)\,dx\] としてもよい.要するに関数の値を長方形の右側の辺にとるか左側の辺にとるかの違いである.
冒頭の例でいうと,両者の違いは次の図のようになる.

長方形の和として捉える
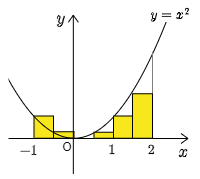
長方形の和として捉える
いずれの場合であっても,$n$ を大きくすればするほど求めたい面積との誤差がどんどん小さくなっていき,$n\to\infty$ の極限において両者は同じ値(求めたい面積)に収束する.
補足2
$\displaystyle \lim_{n\to\infty} \sum_{k=1}^n \dfrac{b-a}n f\left(a+\dfrac{b-a}nk\right)=\int_a^b\!\!f(x)\,dx $ において,左端の境界線である $x=a$ の $a$ が0のとき,
\[\begin{align*}
&x_k=0+\frac {b-0}nk=\dfrac{bk}n,\\[5pt]
&\Delta x=\frac {b-0}n=\dfrac bn
\end{align*}\]
であるから,
\[\lim_{n\to\infty}\sum_{k=1}^n\frac bnf\left(\frac{kb}n\right)=\int_0^b\!f(x)\,dx\]
定積分と和の極限の公式(Ⅰ)\[\lim_{n\to\infty}\sum_{k=1}^n\frac bnf\left(\frac{kb}n\right)=\int_0^b\!f(x)\,dx\]
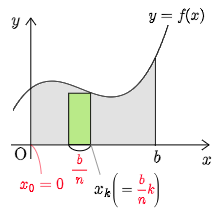
更に $b=1$ のとき,次のようになる.
定積分と和の極限の公式(Ⅱ) 【重要】\[\lim_{n\to\infty}\sum_{k=1}^n\frac 1n f\left(\frac kn \right)=\int_0^1\!f(x)\,dx\]
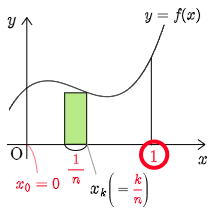
高校数学における区分求積法は,この公式Ⅱに持ち込んで計算するのが基本と思っていて問題ない.つまり,与えられた式を公式Ⅱの左辺と照らし合わせて関数 $f(x)$ を決定するのだ.詳しくは「8.2 いくつかの例題」を参照.

8.2 いくつかの例題
例題1 次の極限を求めよ. \[\lim_{n\to\infty}\sum_{k=1}^n\frac\pi n\sin\frac{k\pi}n\ \ \cdots\mbox{①}\]
このような問題を見ると,数列で学習したいくつかの公式を利用して $\displaystyle \sum$ を具体的に計算してから極限をとりたくなる.実際その方法でも求められる問題もあるのだが,和をとることが困難な場合も多い.$\lim$ と $\displaystyle\sum$ が同時に登場している問題では区分求積法の利用をすぐに思いつけるようにしておきたい.次のイラストで印象付けておこう.