高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | |||
| 5. 置換積分法(定積分) | |||
| 6. 部分積分法(定積分) | |||
| 7. 定積分と微分法 | |||
| 8. 定積分と和の極限 | |||
| 9. 定積分と不等式 | |||
| 10. 定積分の応用(面積) | |||
| 11. 定積分の応用(体積) | |||
| 12. 定積分の応用(回転体の体積) | |||
| 13. 曲線の長さ |

9.定積分と不等式
9.1 定積分と不等式
定理
閉区間 $[a,b]$ で連続な関数 $f(x)$ が,この区間で常に $f(x)\geqq0$ ならば,
\[\int_a^b\!\!f(x)\,dx\geqq0\]
が成り立つ.等号成立は,$[a,b]$ で常に $f(x)=0$ のとき.
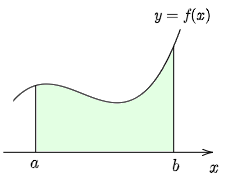
この定理は,図の緑色部分の面積が0以上であるという事実からも理解しやすい.
証明
$\displaystyle{F(x)=\int_a^x\!\!f(t)dt}$ とする.$F(b)\geqq 0$ を示せばよい.
$\displaystyle F'(x)=\frac d{dx}\int_a^x\!\!f(t)dt=f(x)\geqq 0\ \ (\because$ 仮定)
であるから,$F(x)$ は $a\leqq x\leqq b$ で単調に増加する関数である.よって,
\[F(x)\geqq F(a)\left(=\int_a^a\!\!f(t)dt\right)=0\]
により, $F(x)$ は $a\leqq x\leqq b$ で常に非負となり,従って $F(b)\geqq 0$.
また,等号が成立するとき,すなわち $\displaystyle{\int_a^b\!f(x)dx=F(b)=0}$ が成り立つときは,$F(x)$ の単調増加性により
\[0=F(a)\leqq F(x)\leqq F(b)=0\]
となるから,$F(x)$ は $a\leqq x\leqq b$ で常に0.
故に $f(x)=F'(x)=(0)’=0$.
■
系
閉区間 $[a,b]$ で連続な関数 $f(x)$ が,この区間で常に $f(x)\geqq 0$,かつ $\displaystyle{\int_a^b\!f(x)dx=
0}$ ならば,この区間で常に $f(x)=0$.
証明
上の定理の証明における等号成立時の議論により明らか.
■
上の定理から,直ちに次が成り立つ:
定理
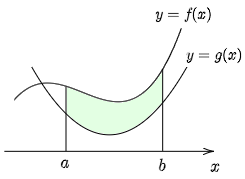
閉区間 $[a,b]$ で連続な関数 $f(x)$ が,この区間で常に $f(x)\geqq g(x)$ ならば,
\[\int_a^b\!\!f(x)\,dx\geqq\int_a^b\!\!g(x)\,dx\]
が成り立つ.等号成立は,$[a,b]$ で常に $f(x)=g(x)$ のとき.
証明
$F(x)=f(x)-g(x)$ とおくと,区間 $[a,b]$ で常に $F(x)\geqq0$.従って,
\[\int_a^b\!\!F(x)\,dx=\int_a^b\!\!\{f(x)-g(x)\}dx\geqq0\]
\[\therefore \int_a^b\!\!f(x)\,dx-\int_a^b\!\!g(x)\,dx\geqq0\]
\[\therefore \int_a^b\!\!f(x)\,dx\geqq\int_a^b\!\!g(x)\,dx\]
■

例題1 次を示せ. \[\frac\pi4 < \int_0^1\!\!\frac{dx}{1+x^3} < 1\]
こたえ
閉区間 $[0,1]$ において,常に
\[1 \leqq 1+x^3\leqq 1+x^2 \]
であるから,
\[\frac1{1+x^2}\leqq\frac1{1+x^3}\leqq 1\]
この不等式の等号は常に成り立っている訳ではないから,各辺を0から1まで積分すると
\[\int_0^1\!\!\frac{dx}{1+x^2} < \int_0^1\!\!\frac{dx}{1+x^3} < \int_0^1\!\!dx\]
この右辺の積分は1である.またこの左辺の積分は $x=\tan\theta$ とおくと,
\[dx=\dfrac{d\theta}{cos^2\theta},\ \ \begin{array}{c|c}
x&0\to 1\\\hline
\theta&0\to\frac\pi4
\end{array}\]
となるから,
\[\begin{align*}
\int_0^1\!\!\frac{dx}{1+x^2}&=\int_0^{\frac\pi4}\frac1{1+\tan^2\theta}\cdot\frac1{\cos^2\theta}d\theta\\[5pt]
&=\int_0^{\frac\pi4}d\theta=\frac\pi4
\end{align*}\]
\[\therefore \frac\pi4 <\int_0^1\!\!\frac{dx}{1+x^3} < 1\]
■

例題2 $n$ を2以上の自然数とするとき,次を示せ. \[1+\frac12+\frac13+\cdots+\frac1n < 1+\log n\]
こたえ
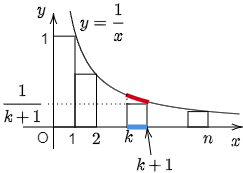
関数 $\dfrac1x$ は $x>0$ で単調に減少するから,任意の自然数 $k$ について,$k\leqq x\leqq k+1$ のとき,
\[\frac1{k+1}\leqq \frac1x\]
が成り立つ.この不等式の等号は常に成り立つ訳ではないから,両辺を $k$ から $k+1$ まで積分すると
\[\int_k^{k+1}\frac{dx}{k+1}< \int_k^{k+1}\frac{dx}x\]
\[\therefore \frac1{k+1}< \int_k^{k+1}\frac{dx}x\]
この式の $k$ に1から $n-1$ まで代入して辺々加えると
\[\frac12\!+\!\frac13\!+\!\cdots\!+\frac1n<\int_1^2\!\!\frac{dx}x\!+\!\int_2^3\!\!\frac{dx}x\!+\!\cdots\!+\!\int_{n-1}^n\!\!\frac{dx}x\]
この右辺は
\[\int_1^n\frac{dx}x=\Bigl[\log |x|\Bigr]_1^n=\log n\]
となるから結局上の式は
\[\frac12\!+\!\frac13\!+\!\cdots\frac1n<\log n\]
この両辺に1を加えて
\[1+\frac12+\frac13+\cdots+\frac1n < 1+\log n\]
■
別解
別解を見る
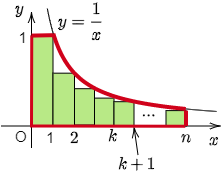
図の長方形の面積の合計より,赤色で囲まれた部分の面積の方が大きいから,
\[\begin{align*}
1+\dfrac12+\dfrac13+\cdots+\dfrac1n& < 1+\int_1^n\!\!\frac{dx}x\\
&=1+\Bigl[\log x\Bigr]_1^n\\
&=1+\log n
\end{align*}\]
■

9.2 絶対値付きの積分不等式
定積分において,被積分関数に絶対値が付いたままでは積分できない.例えば,次の例題を考えてみよう.
例題 次の定積分を求めよ.\[\int_0^3|x-1|dx\]
この問題を
\[\int_0^3|x-1|dx=\left|\,\left[\dfrac{x^2}2-x\right]_0^3\,\right|=\dfrac32\]
と計算したらもちろん間違いである.正しくは $0\leqq x\leqq 1$ において,$x-1\leqq0$ であり,$1\leqq x\leqq3$ において $x-1\geqq0$ であるから