高校数学[総目次]
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | |||
| 2. 導関数 | |||
| 3. 接線 | |||
| 4. 関数の値の変化 | |||
| 5. 極大・極小 | |||
| 6. 関数のグラフと方程式・不等式 |
| 7. 不定積分 | |||
| 8. 定積分 | |||
| 9. 様々な定積分 | |||
| 10. 面積 |

1. 微分係数
1.1 平均変化率
平均変化率とは何か
1次関数 $y=2x+3$ を例にとると,変化の割合すなわち
変化の割合$=\dfrac{y\mbox{の増加量}}{x\mbox{の増加量}}$
は $x$ の値が「どこからどこまで増加するのか」という制限がなく常に2である.ところが一般の関数ではそうはいかない.
例えば2次関数 $y=x^2$ は $x$ の値が1から4まで3だけ増加したとき,それに伴って $y$ は1から16まで15だけ増加するから,変化の割合は $\dfrac{15}3=5$ である.一方 $x$ を同じ3だけ増加させるといっても,例えば0から3まで増加させるとき,$y$ は0から9まで9だけ増加するから,変化の割合は $\dfrac93=3$ となって先程の5と一致していない.
このように,一般の関数では $x$ の値を「①どこから」「②どこまで」増加させるかの2つの要素によって,変化の割合は変わってくるのである.
そこで新しい用語として 平均変化率 を導入する.これは変化の割合の発展版ともいえるもので,「$x$ が $a$ から $b$ まで変化する」という情報を取り入れた次の式で定義される:
平均変化率 $=\dfrac{f(b)-f(a)}{b-a}$
この式を関数 $f(x)$ の $x$ の値が $a$ から $b$ まで変化したときの平均変化率というのである.
補足
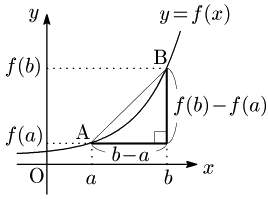
平均変化率は,$f(x)$ のグラフ上の2点を通る直線(図では直線AB)の傾きを表す.
例題 $f(x)=x^2$ のとき,$x$ が1から2まで変化したときの $f(x)$ の平均変化率を求めよ.
平均変化率$=\dfrac{2^2-1^2}{2-1}=\underline{\boldsymbol{3}}$

1.2 極限値
極限値とは何か
例えば,関数 $f(x)=x+1$ を考える.この $x$ の値を,1と異なる値をとりながら限りなく1に近づけると,$f(x)$ はどのような値に近付いていくだろうか?
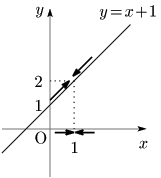
グラフからもわかるように,$f(x)$ は 2 に限りなく近付く.同様に考えて,$x$ が限りなく2に近付けば, $f(x)$ は 3 に限りなく近付くし, $x$ が $-1$ に限りなく近付けば,$f(x)$ は 0 に限りなく近付く.
一般に,関数 $f(x)$ において,$x$ が $a$ と異なる値をとりながら $a$ に限りなく近付くとき,それに応じて $f(x)$ が $\alpha$ に限りなく近付くならば,$\alpha$ を $\boldsymbol x$ が $\boldsymbol a$ に限りなく近付くときの $\boldsymbol{f(x)}$ の極限値といい,
\[\lim_{x\to a}f(x)=\alpha\]
または,
$x\to a$ のとき,$f(x)\to\alpha$
で表す.

●定数関数の極限値
例えば関数 $f(x)=2$ というのは,どんな $x$ の値に対しても2の値をとるような関数で,このような関数を定数関数という.この関数は $x$ をどのような値に近づけようとも極限値が常に2になるというのは明らかである.
定数関数の極限値 $f(x)=c$ ($c$ は定数) のとき,\[\lim_{x\to a}f(x)=c\]
例
\[\lim_{x\to5}4=4\]
注意
極限値は存在しないこともある
例えば,$f(x)=\dfrac1{x^2}$のとき,${\displaystyle\lim_{x\to0}}\ f(x)$ は値がどんどん大きくなるため,一定の値に限りなく近付かない.従ってこの場合の極限は存在しない.(極限値は $\infty$ というのは間違い.「$\infty$」は値ではない.)
発展的注意
「$\displaystyle\lim_{x\to a} f(x)$ を求めることは $f(a)$ を計算することである」は必ずしも正しくない
細かい注意をしておくと,先の $f(x)=x+1$ では $\displaystyle\lim_{x\to1} f(x)=2$ になり,これは $f(1)=2$ と一致する.同様に,$\displaystyle\lim_{x\to2} f(x)=3$ は,$f(2)=3$ と等しく,$\displaystyle\lim_{x\to -1} f(x)=0$ は,$f(-1)=0$ と等しい.この結果を見ると「$\displaystyle\lim_{x\to a} f(x)$ を求めることは,$f(a)$ を計算することではないか」と思ってしまうかもしれないが,これは必ずしも正しくない.例えば関数 $g(x)=\dfrac{x^2-1}{x-1}$ において, $x$ の値を限りなく1に近づけてみよう.この関数の (分母)$=x-1\neq0$ より $x$ は1をとれないから,$\boldsymbol{ g(1)}$ などというものは考えられない.しかし $x$ が1と異なる値をとる限りにおいて,
\[g(x)=\dfrac{x^2-1}{x-1}=\dfrac{(x+1)(x-1)}{x-1}=x+1\]
となり,関数の値は $x+1$ の値と一致する.
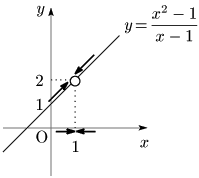
従って,グラフからもわかるように,$g(x)=\dfrac{x^2-1}{x-1}$ の $x$ を,1と異なる値をとりながら限りなく1に近づけると,$g(x)$ は限りなく2に近付くのである.
つまり,極限値とは関数が限りなく近付く値であって,関数がその値をとれるかどうかには全く関心がない.ほとんど同じ例だが,
\[f(x)=\left\{
\begin{array}{ll}
x+1&(x\neq1)\\
5&(x=1)
\end{array}\right.\]
は,$x$ が1と異なる値をとりながら限りなく1に近付くとき,$f(x)$ は限りなく2に近付く.
極限値とは要するに関数の「目的値」である.その関数が向かっていく先のゴール地点を表したものが極限値であると理解しておこう.
極限値は関数の「目的値」である.
※ この辺りの事情は数学Ⅲ 関数の連続性 で詳しく学ぶ.

1.3 微分係数

関数 $f(x)$ の $x$ が $a$ から $b$ まで変化したときの平均変化率とは次のようなものであった: