置換積分法(不定積分)具体例から始めてわかりやすく解説

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質
5. 置換積分法（定積分）
6. 部分積分法（定積分）
7. 定積分と微分法
8. 定積分と和の極限
9. 定積分と不等式
10. 定積分の応用（面積）
11. 定積分の応用（体積）
12. 定積分の応用（回転体の体積）
13. 曲線の長さ

2．置換積分法(不定積分)

2.1　$\displaystyle\int\!f(ax+b)dx$ の計算

数学Ⅱの積分法でよくある例題

次の例題は，数学Ⅱの積分法でしばしば見かける問題である．

例題　放物線 $y=4x^2-11x+8$ と，この放物線上の点 $\left(\dfrac32,\ \dfrac12\right)$ における接線 $y=x-1$，及び $y$ 軸とで囲まれた部分の面積 $S$ を求めよ．

こたえ

　図の色付けされた部分の面積が $S$ であるから，

\[\begin{align*}
S&=\int_0^{\frac32}\{(4x^2-11x+8)-(x-1)\}\,dx\\[5pt]
&=\int_0^{\frac32}(4x^2-12x+9)\,dx\\[5pt]
&=\left[\dfrac43x^3-6x^2+9x\right]_0^{\frac32}\,dx\\[5pt]
&=\dfrac43\left(\dfrac32\right)^3-6\left(\dfrac32\right)^2+9\cdot\dfrac32\\[5pt]
&=\dfrac43\cdot\dfrac{27}8-6\cdot\dfrac94+\dfrac{27}2\\[5pt]
&=\dfrac92-\dfrac{27}2+\dfrac{27}2\\[5pt]
&=\dfrac92
\end{align*}\]

　計算手順が多く，分数計算がミスを誘うが，この程度なら手の運動といったところだ．

　ところでこの定積分の被積分関数 $4x^2-12x+9$ は，$(2x-3)^2$ と因数分解できるから，面積 $S$ は

\[S=\int_0^{\frac32}(2x-3)^2\,dx\]

という簡素な姿に還元できる．この式を遠巻きに眺めると，どこか $\displaystyle\int_0^{\frac32} x^2\, dx$ の残像が微かに漂っているのを感じ取れる．$\displaystyle \int x^2\,dx=\dfrac{x^3}3+C$ $(C$ は定数) という公式の誘惑に抗えず，「えい，や！」とばかりに模倣を試みると，

\[\left[\dfrac{(2x-3)^3}3\right]_0^{\frac32}=0-(-9)=9\]

という結果に辿り着く．正答は得られなかったが，正しい値 $\dfrac92$ のちょうど2倍という，当たらずとも遠からずの結果である．しかし，正しさに近づいたかのようなこの種の錯覚は，むしろ滑稽と言うほかない．距離の遠近にかかわらず，面積 $S$ を正しく導き得ていないという1点において，すべては同じ穴のムジナだ．仮に偶然にも $\dfrac92$ という値に到達したとしても，その計算に正当性の根拠がなければ，数学的には何ら意味を持たない．上の計算はありふれたインチキ計算の1つに過ぎないのである．

インチキが本物に変わる“2”の魔法

　しかし実のところ，面積 $S$ の計算において，先ほど「インチキ計算」と断じられた手続きも，わずかな修正を施すだけで，たちまち数学的正当性を纏うことになる．その手順は次の通り．

\[\begin{align*}
S&=\int_0^{\frac32}(2x-3)^2\,dx\\[5pt]
&=\left[\dfrac{(2x-3)^3}{\color{red}{2}\cdot3}\right]_0^{\frac32}\\[5pt]
&=0-\left(-\dfrac92\right)\\[5pt]
&=\dfrac92
\end{align*}\]

すなわち，計算の過程で $(\color{red}{2}x-3)^2$ の $\color{red}{2}$ で割っておく，ただそれだけの控えめな操作である．そしてこの「2」は，決して結果から逆算して都合よく置かれたものではなく，論理の必然がそこに導いたものである．まずいスープが，魔法のつえひと振りで至福の一皿へと変貌するかのように，計算の煩雑さは一瞬にして消え去り，計算エラーの危険性もまた，同時に遠ざかる．この手つきは，単なる技巧にとどまらず，計算という営為における必然として，是非とも身につけておきたい．

　ではこの「2」が，単なる偶然や恣意ではなく，どのような論理的要請から導かれたものなのか．その正しさの所在を，次に明らかにしていくこととしたい．

置換積分法の特別な形

　$F(x)$ を関数 $f(x)$ の不定積分(原始関数)の1つとする．すなわち $F'(x)=f(x)$ である．
　いま，この $F(x)$ と $ax+b$ という2つの関数を合成した関数である $F(ax+b)$ を微分することを考える．合成関数の導関数の公式
から

\[\begin{align*}
\{F(ax+b)\}’&=F'(ax+b)\cdot (ax+b)’\\[5pt]
&=F'(ax+b)\cdot a\\[5pt]
&=f(ax+b)\cdot a
\end{align*}\]

\[\therefore \ \ \{F(ax+b)\}’=a\,f(ax+b)\]

　この両辺を $a$ で割って

\[\left\{\frac1aF(ax+b)\right\}’=f(ax+b)\]

を得る．この式は，$\dfrac1aF(ax+b)$ を微分すると，$f(ax+b)$ が導かれることを示している．換言すれば，$\dfrac1aF(ax+b)$ は $f(ax+b)$ の不定積分であるということに他ならない．従って次が成り立つ：

補足

　$ax+b=u$ とおくと，$(*)$ は
\[\int\!f(u)\,dx=\frac1{u’}F(u)+C\]

という形で簡素に書ける．

重要例題　$\displaystyle\int (ax+b)^n\,dx$ を計算せよ．

答え

　被積分関数である $(ax+b)^n$ を，$\begin{cases}
f(u)=u^n\\[5pt]
u=ax+b
\end{cases}$ という2つの関数の合成関数であると捉える．また，$F(u)$ を $f(u)$ の原始関数，すなわち $F'(u)=f(u)$ であるとする．

\[\begin{align*}
\mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt]
&=\frac1a\cdot\frac1{n+1}u^{n+1}+C\\[5pt]
&=\underline{\frac1{a(n+1)}(ax+b)^{n+1}+C}
\end{align*}\]

　特に $a=1$ の場合の次の式は，数学Ⅲを学ばない文系の人たちにも是非使えるようになっておいてほしい．計算スピードと正確性が劇的に向上するので必須の公式としておきたい：

例1　$\displaystyle\int\!\cos(2x+3)dx$

　$\left\{\begin{array}{l}
f(u)=\cos u\\
u=2x+3
\end{array}\right.$ とおくと，
\[\begin{align*}
\mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt]
&=\frac12\sin u+C\\[5pt]
&=\underline{\frac12\sin(2x+3)+C}
\end{align*}\]

例2　$\displaystyle\int\!2e^{-3x+4}dx$

　$\left\{\begin{array}{l}
f(u)=2e^u\\
u=-3x+4
\end{array}\right.$とおくと，
\[\begin{align*}
\mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt]
&=\frac1{-3} 2e^u+C\\[5pt]
&=\underline{-\frac23 e^{-3x+4}+C}
\end{align*}\]

2.2　置換積分法

置換積分法の具体例

　積分変数を別の変数に変換(置換)する積分方法を，置換積分法という．置換積分法によって，積分変数を別なものに変えることで，積分できなかった関数が積分できるようになることがある．

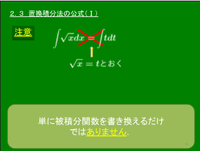
例題　次の不定積分を求めよ． \[y=\int\!\sqrt x\,dx\ \ \cdots\mbox{①}\]

やり方その1