高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

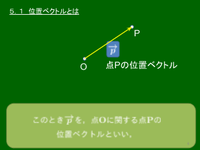
5. 位置ベクトル
5.1 位置ベクトルとは?
ベクトルというものは,向きと大きさを持った量であり,有効線分(平たく言えば矢印)によって表現できることを最初に学んだ(ベクトルと有効線分 ).したがってベクトルは,有効線分の向きと大きさが同じであれば,それが平面上のどこに描かれていようとベクトルとしては同じものである.例えば次の図において,
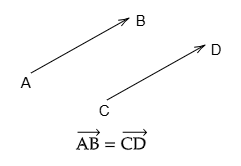
ベクトルとしては同じもの
始点を固定すれば,あとは終点のみ
今,平面上に点Oを任意の場所に取って固定しよう.座標軸が設定されているなら点Oは原点であるとイメージしていてもよい.そして今後この平面上でベクトルを考える際には,常にこの点Oを始点にすると約束しよう.するとあとは終点の位置を決めればベクトルが決定される.逆に,ベクトル(有効線分)を決めれば,始点がOに重ねるように平行移動することで,終点の位置が決まる.即ち
ベクトルの終点=点の位置
という関係が成立する.同じことだが,
ベクトルの終点と平面上の点が1対1に対応する
と言い換えることもできる.ベクトルによって平面上の点の位置を表すことができるのである.
一般に,平面上において点Oを任意の位置に固定し,どのベクトルも常にこの点Oを始点にすると決めれば,平面上の任意の点Pの位置は,
例
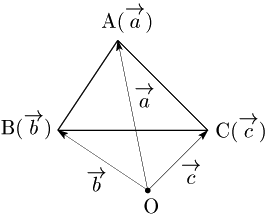

5.2 分点の位置ベクトル
内分点
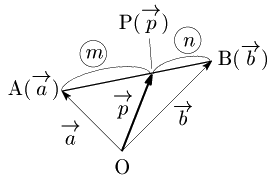
線分ABを
外分点
線分ABを
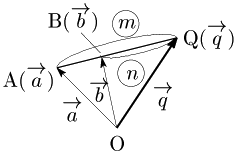
Bは線分AQを
内分点,外分点の位置ベクトル 2点
例題 △ABCの重心Gの位置ベクトル
答
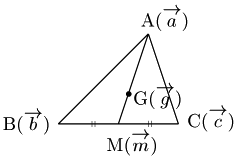
辺BCの中点を
三角形の重心の位置ベクトル 3点

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |