10. 空間ベクトルの内積【ノート】
1人で学べる！高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート	問題
1. ベクトルと有向線分
2. ベクトルの演算
3. ベクトルの成分
4. ベクトルの内積
5. 位置ベクトル
6. ベクトル方程式
7. 平面ベクトルの応用
8. 空間ベクトル
9. 空間ベクトルの成分
10. 空間ベクトルの内積
11. 空間の位置ベクトル
12. 空間ベクトルの応用
13. 空間のベクトル方程式

10.　空間ベクトルの内積

10.1　空間ベクトルの内積

　空間内の$\overrightarrow{0}$でない2つのベクトル$\overrightarrow{\mathstrut a},\ \overrightarrow{b}$のなす角を$\theta$とすると， $$\overrightarrow{\mathstrut a}\cdot\overrightarrow{b}=|\overrightarrow{\mathstrut a}||\overrightarrow{b}|\cos\theta\ \ (0^\circ\leqq\theta\leqq180^\circ)$$

補足

　$\overrightarrow{\mathstrut a}=\overrightarrow{0}$，または$\overrightarrow{b}=\overrightarrow{0}$のとき，$\overrightarrow{\mathstrut a}\cdot\overrightarrow{b}=0$と定義する．

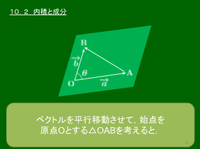
10.2　内積と成分

　$\overrightarrow{\mathstrut a}=(a_1,\ a_2,\ a_3),\ \overrightarrow{\mathstrut b}=(b_1,\ b_2,\ b_3)$ のとき，
$[1]\ \ \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1b_1+a_2b_2+a_3b_3$
$[2]\ \ \overrightarrow{\mathstrut a}\!\neq\!\overrightarrow{0}$，$\overrightarrow{\mathstrut b}\!\neq\!\overrightarrow{\mathstrut 0}$ のとき，$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角を $\theta$ とすると， $$\begin{align*} \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\ &=\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}\sqrt{{b_1}^2+{b_2}^2+{b_3}^2}} \end{align*}$$

[1]の証明

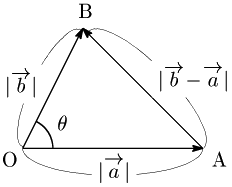
　余弦定理により，

AB$^2=$ OA$^2+$ OB$^2-2$ OA$\cdot$OB $\cos\theta$

$$\therefore |\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}$$

$\therefore \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=\dfrac{|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2}2\ \ \cdots$ ①

(①の右辺の分子)$=({a_1}^2\!+\!{a_2}^2\!+\!{a_3}^2)\!+\!({b_1}^2\!+\!{b_2}^2\!+\!{b_3}^2)$
　　　　　　　　　$-\{(b_1\!-\!a_1)^2\!+\!(b_2\!-\!a_2)^2\!+\!(b_3\!-\!a_3)^2\}$
　　　　　　　　$=2(a_1b_1+a_2b_2+a_3b_3)$

よって①より，

$$\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1b_1+a_2b_2+a_3b_3$$

■

例題　$\overrightarrow{a}=(-1,\ 2,\ -2),\ \overrightarrow{b}=(2,\ -2,\ 3)$の両方に垂直で，大きさが3であるベクトル$\overrightarrow{p}$を求めよ．

　$\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$ の双方に垂直なベクトルの1つを $\overrightarrow{\mathstrut q}=(x,y,z)$ とすると，

　$\overrightarrow{\mathstrut q}\perp\overrightarrow{\mathstrut a}$ より $\overrightarrow{\mathstrut q}\cdot\overrightarrow{\mathstrut a}=0$
　　　$\therefore -x+2y-2z=0\ \ \cdots$ ①

　$\overrightarrow{\mathstrut q}\perp\overrightarrow{\mathstrut b}$ より $\overrightarrow{\mathstrut q}\cdot\overrightarrow{\mathstrut b}=0$
　　　$\therefore 2x-2y+3z=0\ \ \cdots$ ②

　①$+$② より，$x+z=0$　$\therefore x=-z\ \ \cdots$ ③
　①$\times2+$② より，$2y-z=0$　$\therefore y=\dfrac z2\ \ \cdots$ ④

　③，④ で $z=2$ とおくと，$\overrightarrow{\mathstrut q}=(-2,1,2)$

　よって， $$\begin{align*} \overrightarrow{\mathstrut p}&=\pm3\cdot\frac{\overrightarrow{\mathstrut q}}{|\overrightarrow{\mathstrut q}|}=\pm3\cdot\dfrac{(-2,1,2)}3\\[5pt] &=\underline{\boldsymbol{\pm(-2,1,2)}} \end{align*}$$

補足

　$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の双方に垂直なベクトルの1つを $\overrightarrow{\mathstrut q}$ とすると，次のような計算によって $\overrightarrow{\mathstrut q}$ を求めることができる．(詳しくはスライド(会員向け)参照．)

$$\begin{align*} \overrightarrow{\mathstrut q}&=\Bigl(2\!\cdot\!3\!-\!(-2)\!\cdot\!(-2),\ (-2)\!\cdot\!2\!-\!(-1)\!\cdot\!3,\ -1\!\cdot\!(-2)\!-\!2\!\cdot\!2\Bigr)\\[5pt] &=(2,\ -1,\ -2) \end{align*}$$

　実際，

$$\begin{align*} \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut q}&=(-1,2,-2)\cdot(-2,1,2)=2+2-4=0\\[5pt] \overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut q}&=(2,-2,3)\cdot(-2,1,2)=-4-2+6=0\\[5pt] \end{align*}$$

となるから $\overrightarrow{\mathstrut a}\perp\overrightarrow{\mathstrut q}$ かつ $\overrightarrow{\mathstrut b}\perp\overrightarrow{\mathstrut q}$ である．

　$\overrightarrow{\mathstrut q}$ を $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の外積またはベクトル積という．ベクトル積は，2つのベクトルから1つのベクトルが返される．一方，内積は2つのベクトルから1つの実数が返される．従って内積のことをスカラー積ともいう．

10.3　内積の性質

$$\begin{align*} &[1]\ \ \overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{\mathstrut{a}}\ \ (\mbox{交換法則})\\[5pt] &[2]\ \ \overrightarrow{a}\cdot\overrightarrow{a}=\left|\overrightarrow{a}\right|^2\\[5pt] &[3]\ \ \overrightarrow{\mathstrut{a}}\cdot(\overrightarrow{b}+\overrightarrow{\mathstrut{c}})=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}+\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[4]\ \ (\overrightarrow{\mathstrut{a}}+\overrightarrow{b})\cdot\overrightarrow{\mathstrut{c}}=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}+\overrightarrow{b}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[5]\ \ (k\overrightarrow{\mathstrut{a}})\cdot\overrightarrow{b}=\overrightarrow{a}\cdot(k\overrightarrow{b})=k(\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b})\ \ (k\mbox{ は実数}) \end{align*}$$

補足

　平面ベクトルの内積の性質と完全に同一である．

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート	問題
1. ベクトルと有向線分
2. ベクトルの演算
3. ベクトルの成分
4. ベクトルの内積
5. 位置ベクトル
6. ベクトル方程式
7. 平面ベクトルの応用
8. 空間ベクトル
9. 空間ベクトルの成分
10. 空間ベクトルの内積
11. 空間の位置ベクトル
12. 空間ベクトルの応用
13. 空間のベクトル方程式