高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

12. 空間ベクトルの応用
12.1 一直線上の3点
3点A,B,Cが一直線上
となる実数 が存在

12.2 平面上の点
空間内の一直線上にない3点A,B,Cが与えられると,それら3点を含む平面が存在し,かつそのような平面はただ1つである.この平面を平面ABCという.
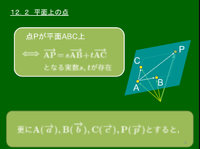
平面上の点Pについては次が重要:
点Pが平面ABC上
となる実数 が存在
,,, とすると,上の式は
ここで, とおくと,
がこのように表されるとき,この表し方はただ1通りであり,次が成立:
について, と表されるとき,
点Pが平面ABC上
例題 図のような直方体において,DEの延長上に DEEF となる点Fをとる.直線OFと平面ABCの交点をPとするとき, を ,, で表せ.
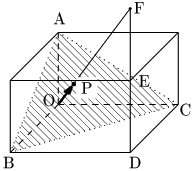

答
従って,
点Pは平面ABC上にあるから,
よって,

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |