受験数学において,「ファクシミリの原理」と呼ばれる魅力的な考え方があります.「大学への数学(東京出版)」で用いられている大変印象的な用語で,考え方の本質を「ファクシミリ」になぞらえているところがユニークでもあります.
ファクシミリの原理という考え方の基本は,簡単な例題を用いてスライド で解説していますのでそちらをご覧ください.ここでは京都大学と東京大学の本格的な問題を用いて,自然な発想でのやり方と,ファクシミリの原理を用いたやり方の2通りで説明してみます.
付録として,包絡線を用いた考え方も紹介しています.
高校数学[総目次]
高校数学ワンポイント

1.京都大学の過去問
答その1 [自然な発想]
$L:y=2x\ (0\leqq x\leqq1)$ と表されますから,曲線 $y=x^2+ax+b$ が $L$ と共有点をもつための条件は,2次方程式 $x^2+ax+b=2x$ 即ち
\[x^2+(a-2)x+b=0\]
が,$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことです.
$f(x)=x^2+(a-2)x+b$ とおくと,放物線 $y=f(x)$ は下に凸で,軸は直線 $x=-\dfrac{a-2}2$ です.
方程式 $f(x)=0$ が $0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつのは,次の[1], [2] の場合が考えられます:
[1] $f(0)=0$ または $f(1)=0$ のとき,即ち $b=0$ または $a+b-1=0$ のとき
このときは題意を満たします.
[2] $f(0)\neq0$ かつ $f(1)\neq0$ のとき,即ち $b\neq0$ かつ $a+b-1\neq0$ のとき
$1^\circ$ 重解を含む2解がともに $0 < x < 1$ の範囲にあるとき
このとき,$f(x)=0$ の判別式を $D$ とすると,
\[\begin{align*}
&\begin{cases}
D=(a-2)^2-4b\geqq0\\[5pt]
\mbox{軸}:0 < -\dfrac{a-2}2 < 1\\[5pt]
f(0)=b > 0\\[5pt]
f(1)=a+b-1 > 0
\end{cases}\\[5pt]
\\
\therefore\ \ &
\begin{cases}
b\leqq \dfrac{(a-2)^2}4\\[5pt]
0 < a < 2\\[5pt]
b > 0\\[5pt]
b > -a+1
\end{cases}
\end{align*}\]
$2^\circ$ $0 < x < 1$ にただ1つの解をもつとき
$f(0)f(1) < 0$ 即ち $b(a+b-1) < 0$
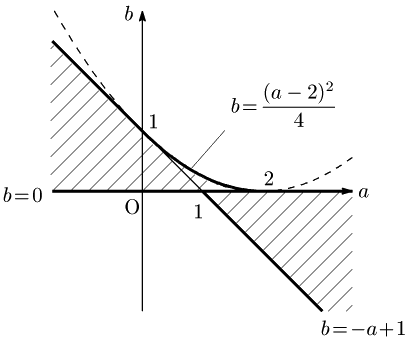
以上により,実数の組 $(a,b)$ の集合は,図の斜線部分のようになります.ただし境界線を含みます.
補足1
2次方程式の解の配置については,数学Ⅰ 第1章 2次関数 7. 2次方程式の解の配置のスライド,及び【ノート】をご覧ください.
補足2
上の方法では2次方程式 $x^2+(a-2)x+b=0$ が,$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことを直接に求めましたが,否定の範囲を計算してその補集合を考えるのでもよいでしょう.この場合否定は「2次方程式 $x^2+(a-2)x+b=0$ が,$0\leqq x\leqq1$ の範囲に解を持たない」となりますから,その条件は $f(x)=x^2+(a-2)x+b$ とおくと
$\mbox{min}\left\{f(0),\ f(1),\ f\left(-\dfrac{a-2}2\right)\right\}>0$ または
$\mbox{max}\left\{f(0),\ f(1)\right\}<0$
即ち
「$b\!>\!0$ かつ $a\!+\!b\!-\!1\!>\!0$ かつ $b\!-\!\dfrac{(a-2)^2}4\!>\!0$」または
「$b<0$ かつ $a+b-1<0$」
です.ただし $f\!\left(\!-\dfrac{a\!-\!2}2\right)$ は,放物線の軸が定義域内に入っている $0\leqq-\dfrac{a-2}2\leqq1$ 即ち $0\leqq a\leqq 2$ の範囲のみで有効になります.この範囲を図示すれば,上図の斜線が施されていない部分となります.ただし境界線は含みません.
※ max,min の部分の詳しい考え方については,数学Ⅰ 第1章 2次関数 3. 2次関数の最大・最小のスライド ,及び ノート をご覧ください.

答その2 [ファクシミリの原理]
$x^2+(a-2)x+b=0\ \cdots$ ① が $0\leqq x\leqq 1$ の範囲に少なくとも1つの解をもつ $(a,\ b)$ の条件を求めればよいわけですが,そのために①を変形して
$b=-x^2-(a-2)x\ \cdots$ ②
としておきます.そして次がファクシミリの原理という考え方のポイントです.
$\boldsymbol{a}$ を固定する
すると,②の右辺は $x$ の2次関数であり.これを $f(x)$ とおくとき,
$\boldsymbol{b=f(x)}$ の値域を調べる
ということを行います.このように固定した値に対して値域を探るという手法を「ファクシミリの原理」と呼んでいるわけです.
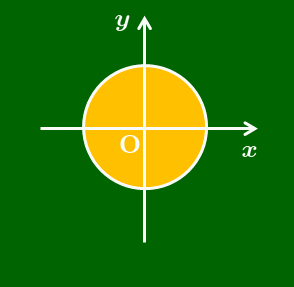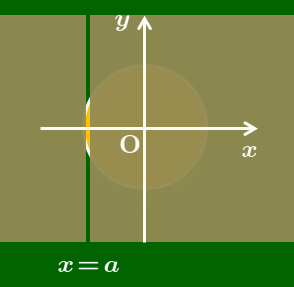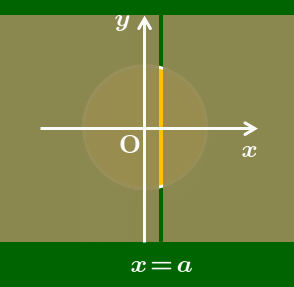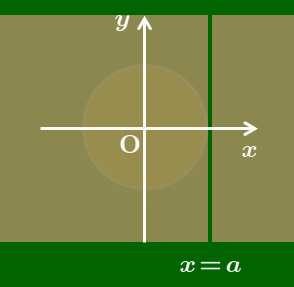
これをイメージとして捉えると次のようになります.座標平面というキャンバスに幾何学的な模様が描かれているとします.しかしシートで全体が覆われており,その模様が見えません.シートには小さなスリットが1つあり,この隙間部分だけは見えていますが,細すぎて全体像がつかめません.幸い,このシートは $x$ 軸方向に移動可能だったので,右側にずらしていくと,隠れていた模様が少しずつ見えて全体像をつかむことができます.