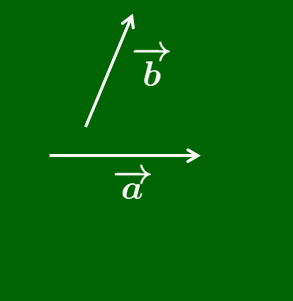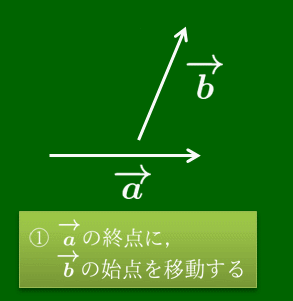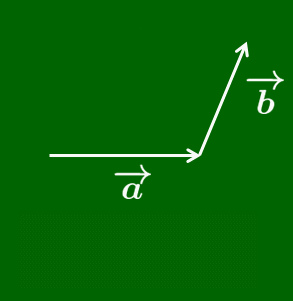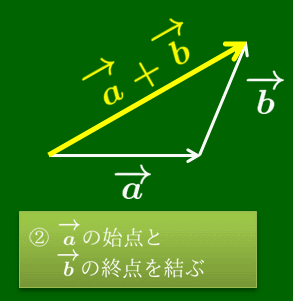高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

2. ベクトルの演算
2.1 ベクトルの加法
「向き」と「大きさ」を同時に持つ量をベクトルと呼んだが,これらに実数のときにあったような加減乗除,すなわち足したり引いたり掛けたり割ったりといった計算ができるのであろうか.
足し算・引き算はベクトルにも存在する.また,ある種の掛け算も存在する.
しかしベクトルの割り算は存在しない.
加減乗除のうち「加減乗」はあるが,「除」だけはないのである.
それではベクトルの足し算である加法からみていこう.
ベクトルどうしの足し算とは?
2つのベクトル $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ について,$\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}$ のような量を考えたい.どのように導入すればよいだろうか.
ベクトルには向きと大きさがあったから,大きさだけをみて,その和を考えるのであろうか?
例として床に大きな荷物があるとしよう.
これをAさんが右向きに4の力で引っ張ったが動かなかったので,通りかかったBさんに助けを求めた.
そこでBさんは3の力で手伝ったところ,荷物が動き出した.
このとき,2人は合計で4+3=7の力で引っ張ったことになる.
それでは次はどうだろう.
机の上に消しゴムを置いて,右向きに4の力で引っ張り,同時に上向きに3の力で引っ張るとしよう.
さてこの消しゴムはどの方向にどんな力で引っ張られて行くであろうか.
実はこのとき,対角線の方向に5の力で引っ張られることになる.単純に4+3で7とはならない.(下のアニメーション参照)
また次のように述べることもできる.次の2つは,消しゴムに対して全く同じ作用を及ぼすことになる:
- 右方向に4,上方向に3という2つの力を加えること
- 対角線の方向に5という力を1つだけ加えること

1つの力だけで表すことができる.
ベクトルの加法とは
先の消しゴムの例で見たように,ある物体に対して異なる向きに2つの力を加えると,その2つのどちらとも異なる向きに力を加えていることになる.
その向きとは消しゴムの例では長方形の対角線の方向であったが,一般には2つ有向線分を2辺とする平行四辺形の対角線の方向になる.
そして力の大きさは対角線の長さとなる.
これを数学的に表現したものがベクトルの足し算である加法だ.
2つのベクトル $\overrightarrow{\mathstrut a},\, \overrightarrow{\mathstrut b}$ について,それらを始点をそろえて有向線分で表したとき,その2辺でできる平行四辺形の向き付き対角線を $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の和といい,$\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}$ で表す.
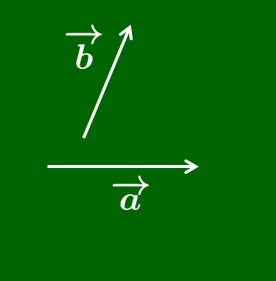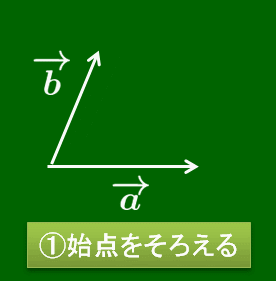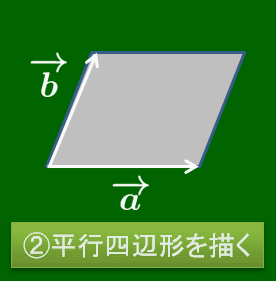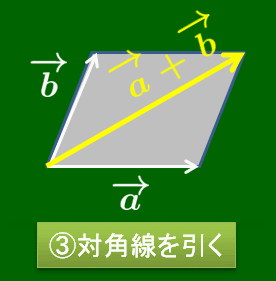
あるいは次のように考えることもできる.ベクトルは描く位置にはよらなかったので,$\overrightarrow{\mathstrut a}$ の終点に $\overrightarrow{\mathstrut b}$ の始点を重ね,$\overrightarrow{\mathstrut a}$ の始点から$\overrightarrow{\mathstrut b}$ の終点に伸びる有向線分が表すベクトルを $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の和といって,$\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}$ で表すのだ.