ベクトル方程式の基本｜直線・円の表し方と媒介変数の意味をスライドでやさしく解説

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート	問題
1. ベクトルと有向線分
2. ベクトルの演算
3. ベクトルの成分
4. ベクトルの内積
5. 位置ベクトル
6. ベクトル方程式
7. 平面ベクトルの応用
8. 空間ベクトル
9. 空間ベクトルの成分
10. 空間ベクトルの内積
11. 空間の位置ベクトル
12. 空間ベクトルの応用
13. 空間のベクトル方程式

6．ベクトル方程式

　等式には方程式と恒等式があって，方程式とは特定の値でのみ成立する等式，恒等式とはいかなる値でも成立する等式である．方程式の例としては $y=2x+3$ などで，この方程式を満たす $(x,\ y)$ の組として $(0,\ 3)$，$(1,\ 5)$ などがあり，すべての組を座標平面上に取っていくと，そこに現れる図形は直線である．このような方程式をベクトルにまで拡張しよう．

6.1　直線のベクトル方程式

直線のベクトル方程式は，ちょっとした思考の転換が必要

　これからベクトルによって直線を表そうという訳だが，これまでの $y=mx+n$ の形が頭にあると，かえって理解の邪魔になるかもしれない．$y=mx+n$ は

$x$ が決まる → $y$ が決まる → 点 $(x,\ y)$ が決まる

という流れであり，従って方程式の左辺は「$y=$」となっている場合が多い．一方，ベクトルで直線を表すときには

$t$ が決まる　→　点 $(x,\ y)$ が決まる

といったように， $x,\ y$ の文字以外に点を動かす原動力となる実数 $t$ を介在させている．その結果ベクトル方程式では直線上の点を表す位置ベクトル $\overrightarrow{\mathstrut p}$ が左辺にくる場合が多い．
　このように，ベクトルで直線を表現するには従来とやや異なった思考が必要である．

ではどのようにベクトルで直線を表現するのか

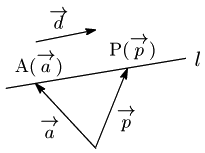
　直線 $l$ は，位置ベクトルが $\overrightarrow{\mathstrut a}$ である点Aを通り，$\overrightarrow{\mathstrut d}(\neq\overrightarrow{\mathstrut 0})$ に平行であるとする．この直線上の点Pについて，その位置ベクトルを $\overrightarrow{\mathstrut p}=(x,\ y)$ とすると

$\overrightarrow{\mathstrut{\rm AP}}=\overrightarrow{\mathstrut 0}$ または $\overrightarrow{\mathstrut{\rm AP}}\ //\ \overrightarrow{\mathstrut d}$

であるから，

点Pが $l$ 上　　　　　　　　　　　
$\iff \overrightarrow{\mathstrut{\rm AP}}=t\overrightarrow{\mathstrut d}$ となる実数 $t$ が存在

が成り立つ．$\overrightarrow{\mathstrut{\rm AP}}=\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a}$ より， \[\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a}=t\overrightarrow{\mathstrut d}\] \[\therefore \overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\] 　これを，点$\boldsymbol{{\rm A}(\overrightarrow{\mathstrut a})}$ を通り，$\boldsymbol{\overrightarrow{\mathstrut d}}$ に平行な直線のベクトル方程式といい，$t$ を媒介変数，$\overrightarrow{\mathstrut d}$ を方向ベクトルという．

直線のベクトル方程式点${\rm A}(\overrightarrow{\mathstrut a})$ を通り，$\overrightarrow{\mathstrut d}(\neq\overrightarrow{\mathstrut 0})$ に平行な直線上の点を ${\rm P}(\overrightarrow{\mathstrut p})$ とすると，この直線のベクトル方程式は\[\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\]

補足

見た目が異なるので直線に見えない…でも中身は同じ

　私たちは $y=mx+n$ の形を直線と理解してきたので，ベクトル方程式を見るとにわかにそれが直線を表しているようには見えない．
　しかし見た目は全く異なっているものの中身は同じで，双方向に変換も可能である．

　1つだけ例を挙げると，直線 $y=\dfrac32x+1$ について，直線上の点として，例えば A$(2,\ 4)$ を考えると，直線上の点の位置ベクトルとして$\overrightarrow{\mathstrut a}=(2,\ 4)$ がとれる．

　また傾きが $\dfrac32$ であるから方向ベクトルとして $\overrightarrow{\mathstrut d}=(2,\ 3)$ がとれる．

　よって直線上の点を表す位置ベクトルを $\overrightarrow{\mathstrut p}=(x,\ y)$ とすれば，