4. 階差数列(ノート) スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学B　第2章　数列

	スライド	ノート	問題
1. 等差数列	[無料]
2. 等比数列	[無料]
3. Σ(シグマ)と和の公式	[無料]
4. 階差数列	[会員]
5. 数列の和と一般項	[会員]
6. 差をとってできる数列の応用	[会員]
7. (等差)×(等比)の和	[会員]
8. 群数列	[会員]		[会員]
9. 隣接2項間漸化式(その1)	[会員]		[会員]
10. 隣接2項間漸化式(その2)	[会員]
11. 隣接3項間漸化式	[会員]		[会員]

4. 階差数列

4.1　階差数列とは

　数列の差をとって得られる数列を，元の数列の階差数列という．

　 $2,\ 3,\ 5,\ 8,\ 12$
　差をとると， $1,\ 2,\ 3,\ 4$
　　→　階差数列は初項1，公差1の等差数列

　 $2,\ 5,\ 11,\ 23,\ 47$
　差をとると， $3,\ 6,\ 12,\ 24$
　　→　階差数列は初項3，公比2の等比数列

　 $2,\ 10,\ 30,\ 68,\ 130,\ 222$
　差をとると， $8,\ 20,\ 38,\ 62,\ 92$
　もう一度差をとると， $12,\ 18,\ 24,\ 30$
　　→　第2階差数列は初項12，公比6の等差数列

補足

　例3のように，複数回にわたって差をとるとき，差をとった順に「第1階差数列，第2階差数列， $\cdots$ 」という．

4.2　階差数列と一般項

階差数列から元の数列の一般項を求める方法～まずは例

　例として次の数列 $\{a_n\}$ を考えよう．

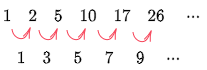
$1,\ 2,\ 5,\ 10,\ 17,\ 26,\ \cdots$

　この数列は差が一定でないから等差数列ではない．また隣りどうしの比も一定ではないから等比数列でもない．従ってこの数列の一般項を直ちに求めることは難しい．ところがこの数列の階差数列をとってみると，

$1,\ 3,\ 5,\ 7,\ 9,\ \cdots$

といった具合に初項1，公差2の等差数列となっており，大変なじみやすいものとなっている．この階差数列を $\{b_n\}$ とおくと，一般項は $b_n=2n-1$ であり，

$\sum_{k=1}^nb_k=\sum_{k=1}^n (2k-1)=n^2$

というように第 $n$ 項までの和も簡単に計算できる．実は階差数列の和が求まれば，得体の知れぬ元の数列の一般項も求めることができる．その考え方を次に示す．

　例えば $a_4=10$ を考えてみよう．

　 $a_4-a_3=b_3$ である．

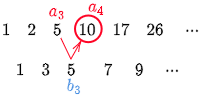
　同様にして，

$\begin{align*} a_4-a_3&=b_3\\[5pt] a_3-a_2&=b_2\\[5pt] a_2-a_1&=b_1\\[5pt] \end{align*}$

　　これらを辺々加えると，左辺は途中で $a_3$ と $a_2$ がキャンセルされて

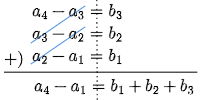
　よって　 $a_4=a_1+(b_1+b_2+b_3)$

　つまり $a_4$ は， $a_1$ に階差数列 $\{b_n\}$ の初項から第3項までの和として求めることができる．これは他の項についても同様である．よって第 $n$ 項の $a_n$ は， $b\geqq2$ のとき

$a_n=a_1+\sum_{k=1}^{n-1}b_k=1+(n-1)^2=n^2-2n+2$

　これは $n=1$ のときも成り立つ．従って数列 $\{a_n\}$ の一般項を求めることができた．

階差数列から元の数列の一般項を求める方法～次に一般論

　上の例のような考え方を用いると，一般の場合は次のようになる：

$\begin{align*} a_n-a_{n-1}&=b_{n-1}\\[5pt] a_{n-1}-a_{n-2}&=b_{n-2}\\[5pt] a_{n-2}-a_{n-3}&=b_{n-3}\\[5pt] &\vdots\\[5pt] a_3-a_2&=b_2\\[5pt] a_2-a_1&=b_1\\[5pt] \end{align*}$

　これらの式を辺々加えると，左辺の $a_{n-1},\ n_{n-2},\ \cdots,\ a_2$ が次々とキャンセルされて，左辺は $a_n$ と $a_1$ だけが残り，右辺は $b_1$ から $b_{n-1}$ までの $n-1$ 項の和となる：

$\therefore\ a_n=a_1+(b_1+b_2+\cdots +b_{n-1})$

　よって第 $n$ 項の $a_n$ は， $b\geqq2$ のとき

$a_n=a_1+\sum_{k=1}^{n-1}b_k$

となる．

　数列 $\{a_n\}$ の初項を $a$ ，階差数列を $\{b_n\}$ とすると， $n\geqq 2$ のとき， $a_n=a+\sum_{k=1}^{n-1}b_k$

補足

$n\geqq2$ の制限について

　一般項を求める式の前に「 $n\geqq2$ のとき」という条件が付されているが，この点について説明しておく．

①　 $n=1$ のとき， $\displaystyle a_1=a+\sum_{k=1}^0 b_k$ となって， $\sum$ が意味をなさない．

②　 $a_1$ の場合が含まれてしまうことがほとんどであるが，もちろんそうでない場合もある．例えば， $2,\ 2,\ 3,\ 4,\ 5,\ 6,\ \cdots\ \ \gets\ \{a_n\}$ という数列の階差数列は $0,\ 1,\ 1,\ 1,\ 1,\ \cdots\ \ \gets\ \{b_n\}$ となるから， $n\geqq2$ のとき， $\begin{align*} a_n&=2+\sum_{k=1}^{n-1}b_k\\[5pt] &=2+(n-2)\\[5pt] &=n \end{align*}$ となる．これは $n=1$ のときを正しく表していない．
　故に， $\underline{\boldsymbol{a_1=2,\ a_n=n\ (n\geqq2)}}$ となる．
　因みに数列 $\{a_n\}$ は，場合分けせずに $a_n=\left|n-\frac32\right|+\frac32$ と書くこともできる．

例題　 $2,\ 5,\ 11,\ 23,\ 47,\ \cdots$ で表される数列の一般項を求めよ．

こたえ

　解答例を表示する

　この数列を $\{a_n\}$ ，階差数列を $\{ b_n\}$ とする．階差数列 $\{ b_n\}$ は次のようになっている： $3,\ 6,\ 12,\ 24,\ \cdots$ 　これは初項3，公比2の等比数列であるから， $b_n=3\cdot2^{n-1}$ ．
　よって $n\geqq 2$ のとき， $\begin{align*} a_n&=2+\sum_{k=1}^{n-1}(3\cdot2^{k-1})\\[5pt] &=2+\frac{3(2^{n-1}-1)}{2-1}\\[5pt] &=3\cdot2^{n-1}-1 \end{align*}$ 　これは $n=1$ のときも成り立つ．
　故に， $\underline{\boldsymbol{a_n=3\cdot2^{n-1}-1}}$

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第2章　数列

	スライド	ノート	問題
1. 等差数列	[無料]
2. 等比数列	[無料]
3. Σ(シグマ)と和の公式	[無料]
4. 階差数列	[会員]
5. 数列の和と一般項	[会員]
6. 差をとってできる数列の応用	[会員]
7. (等差)×(等比)の和	[会員]
8. 群数列	[会員]		[会員]
9. 隣接2項間漸化式(その1)	[会員]		[会員]
10. 隣接2項間漸化式(その2)	[会員]
11. 隣接3項間漸化式	[会員]		[会員]