高校数学[総目次]

数学B　第1章　数列

  スライド ノート 問題
1. 等差数列      
2. 等比数列      
3. Σ(シグマ)と和の公式      
4. 階差数列      
5. 数列の和と一般項      
6. 差をとってできる数列の応用      
7. (等差)×(等比)の和      
8. 群数列      
9. 隣接2項間漸化式(その1)      
10. 隣接2項間漸化式(その2)      
11. 隣接3項間漸化式      

演習問題

問題１【発展】
　2つの関数を$f_0(x)=\dfrac x2,\ f_1(x)=\dfrac{x+1}2$ とおく．$x_0=\dfrac12$ から始め，各 $n=1,\ 2,\ \cdots$ について，それぞれ確率 $\dfrac12$ で，$x_n=f_0(x_{n-1})$ または $x_n=f_1(x_{n-1})$ と定める．
　このとき，$x_n<\dfrac23$ となる確率 $P_n$ を求めよ．

(京都大)

問題１【発展】

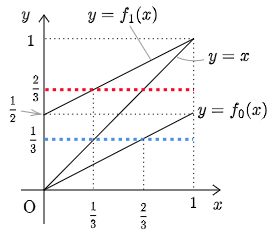
　2つの関数を$f_0(x)=\dfrac x2,\ f_1(x)=\dfrac{x+1}2$ とおく．$x_0=\dfrac12$ から始め，各 $n=1,\ 2,\ \cdots$ について，それぞれ確率 $\dfrac12$ で，$x_n=f_0(x_{n-1})$ または $x_n=f_1(x_{n-1})$ と定める．
　このとき，$x_n<\dfrac23$ となる確率 $P_n$ を求めよ．

(京都大)

　漸化式の基本的な考え方は

最初か最後で場合分け

です．この問題では最後で場合分けするのが良いでしょう．本問を考えやすくするポイントは，グラフによる視覚化です．

　$x_n=f_0(x_{n-1})$ から $x_n$ が決まるときは，確率1で $x_n<\dfrac23$ となり，$x_n=f_1(x_n-1)$ から $x_n$ が決まるときは，$x_{n-1}<\dfrac13$ であれば $x_n<\dfrac23$ となります．となれば，漸化式を作るのにどうしても $x_n<\dfrac13$ となる確率が欲しくなります．

解答