高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

1.ベクトルと有向線分
1.0 矢印クイズ
Q. 1辺の長さが1の方眼紙に,いくつかの矢印があります.

クイズ1 矢印 $a$ と同じ矢印はどれでしょう?
こたえ
矢印 $f$
クイズ2 矢印 $a$ と長さ同じで,向きが逆の矢印はどれでしょう?
こたえ
矢印 $d$
クイズ3 矢印 $a$ と平行な矢印を3つ選びましょう.
こたえ
矢印 $c,\ d,\ f$
クイズ4 長さが1の矢印はどれでしょう?
こたえ
矢印 $b$
1.1 ベクトルとは
これから学ぼうとするベクトルとは一体何を指しているのであろうか.
「ベクトル」という言葉の響き自体が,いかにも「一見さんお断り」といった門前払い的な近寄り難さが漂っている.
中学校ではこのようなカタカナで意味不明な用語は出てこなかった。
「これだから高校数学は…」と青息吐息だ.
ベクトルとは何か(大雑把編)
まずは大雑把にイメージをつかんでおこう.
矢印クイズを用いて説明していく.もしこの全問を軽やかに解き終えることができているなら,その時点で「ベクトルワールド」への入場許可証は掌に収まっているといっても過言ではない.
以後,この矢印を,私たちは「ベクトル」と呼ぶことにする.
これにより,クイズに登場した 6 つの矢印――矢印 $a$ から矢印 $f$――は,それぞれベクトル $a$ からベクトル $f$ と名付け直される.
とはいえ,いちいち「ベクトル $a$ 」と書くのは手が疲れるため,簡単に $\overrightarrow{\mathstrut a}$ と書いて,ベクトル $a$ を表すものとする.
2つのベクトルが等しいというのは,クイズ1で見た通りで,向きと長さが等しい場合をいう.このとき
\[\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut f}\]
と表そう.
次にクイズ2で見た,$\overrightarrow{\mathstrut a}$ と長さは同じだが,向きが正反対であるベクトルを,$\overrightarrow{\mathstrut a}$ の 逆ベクトル といい,
\[-\overrightarrow{\mathstrut a}\]
で表す.つまり「-」は,引き算の意味ではなく「逆向き」の意味であることに注意しよう.
\[\overrightarrow{\mathstrut d}=-\overrightarrow{\mathstrut a}\]
と表すことができる.
クイズ3で見たのと同様に,長さによらず,また向きも考えず,とにかく平行でありさえすれば,ベクトルでも平行である.
最後にクイズ4.長さが1のベクトルを単位ベクトルということにする.ベクトルの長さは | |で表す.つまり,$|\overrightarrow{\mathstrut b}|=1$ である.
ここからは教科書に沿って
先の大雑把編は,本当に大雑把であった.だが,ほんの僅かな修正で,大雑把編はたちまち教科書とほぼ同じ内容となる.
ベクトルというこれまでにない新しい量を,次のように導入する.
ベクトルとは「向き」と「大きさ」という2つの量をあわせもった量をベクトルという
どのような教科書にもこのように説明してあるのだが,さて一体どういう意味なのだろうか?
ベクトルの説明としてしばしば持ち出される例が「速さ」と「速度」である.
●「同じものでしょ?」
さにあらず.
「速さ」が大きさだけをもつ量であるのに対し,「速度」は向きと大きさをもった量,即ちベクトルである.
小学校の算数の文章題では「1分間に50mの速さで歩くと」などと表現されており,速度ではなかったはずだ.それもそのはず,速度はベクトルなので,小学生にとっては難しすぎる用語なのだ.
「速さ」は50mという大きさだけの量である.
一方「速度」は,例えば「西向きに毎分50mの速度で進む」というように,「向き」である西と,「大きさ」である50mを同時に述べなければならない.
このように向きと大きさを一度に表現したとき,その量をベクトルというのである.
●ベクトルの例
力 :右向きに5[N]
速度 :北向きに4m/s
加速度:下向きに9.8m/s$^2$

1.2 有向線分
有向線分はベクトルを表すのに格好の素材
ベクトルを扱っていく上で,大変便利な図形である有向線分を導入する.と言っても単なる矢印のことである.
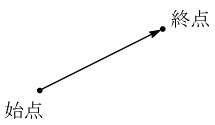
有向線分とは始点と終点を指定した線分を有向線分という.
有向線分は矢印を使って表す.
矢印の根元を始点,先を終点とするのである.
前節で,ベクトルは向きと大きさをもった量であると定義したが,するとベクトルは有効線分を用いて表すことができる.
その表現方法は次のとおりである:
ベクトルの向き :有向線分の向きで表す
ベクトルの大きさ:有向線分の長さで表す
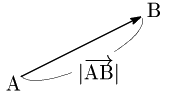
Aを始点,Bを終点とする有向線分を,$\overrightarrow{\mathstrut\rm AB}$ で表し「ベクトルAB」と読む.
またその大きさを $|\overrightarrow{\mathstrut\rm AB}|$ で表す.
要するに矢印の長さを $|\overrightarrow{\mathstrut\rm AB}|$ で表すのである.
※大雑把編では,ベクトルの「長さ」といったが,正式には「大きさ」である.
ベクトル,及びその大きさは,1文字で $\overrightarrow{\mathstrut a}$,$|\overrightarrow{\mathstrut a}|$ などと表すことも多いが,その理由の多くは記述の簡略化のためである.
2つのベクトルが等しいというのはどういうことか
2つのベクトル $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ について,向きと大きさが等しいとき,その2つのベクトルは等しいといい,
\[\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut b}\]
と表す.
ベクトルの相等$\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut b}\iff$ $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ は向きと大きさが等しい.
重要な注意
2つのベクトルが等しいかどうかを判断するとき,位置は問題にしないことに注意する.
つまり平行移動して重なるものは,ベクトルとしては同じものとみなすのである.
これが重要なポイントであるとともに,初学者にとってはわかりにくくもあり,またベクトルでつまずく第1歩もここにある.
ベクトルは向きと大きさだけを指定した量であるから,それがどこに描かれたものであるかは見ないのである.
よくある間違い
$|\overrightarrow{\mathstrut a}|$ は「$\overrightarrow{\mathstrut a}$ の大きさ」と読み,「$\overrightarrow{\mathstrut a}$ の絶対値」とは言わない.
単位ベクトル
大きさが1のベクトルを単位ベクトルという.単位ベクトルは大きさだけを問題にしており,向きは問わない.
補足
大きさのみをもった量をスカラーという.
例 速さ(=速度の大きさ)

番外編
ベクトルのすごさ
ベクトルが何たるかを最初から理解するのは難しい.
とにかくとても便利な道具であることはゆるぎない事実であるが,どう便利なのかは徐々にわかっていくものであろう.
ベクトルのすごさを実感してもらうための例を用意した.とりあえず雰囲気だけ味わってみよう.
●すごさその① 余弦定理
数学Ⅰの三角比で登場する余弦定理.内容は次のようなものであった.
※余弦定理について,詳しくはこちら .
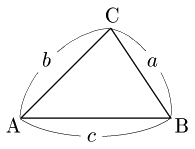
数学Ⅰの三角比のところで記した証明をここに転載すると,次のようなる.三平方の定理を用いただけのものであるが,場合分けも多く,見ての通り証明がとても長い….
数学Ⅰの範囲内での証明
証明を表示する
$a^2=b^2+c^2-2bc\cos A$ を示す.
$A$ が鋭角,直角,鈍角の3通りで場合分けする.
1° $A$ が鋭角のとき
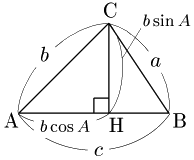
$B$ が鋭角のとき 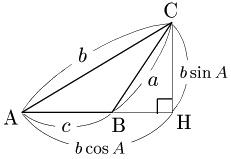
$B$ が鈍角のとき Cから辺ABまたはその延長上に垂線CHを引く.$B$ が鋭角,または鈍角のときは,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\therefore a^2=|c-b\cos A|^2+(b\sin A)^2\] が成り立つ.$B$ が直角の場合は△CBHがつぶれてしまうが, $a=b\sin A$,$c=b\cos A$ であるから上の式はこの場合も含まれる.この式の右辺は \[\begin{align*} &(c^2-2bc\cos A+b^2\cos^2A)+b^2\sin^2A\\[5pt] =&b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A\\[5pt] =&b^2+c^2-2bc\cos A \end{align*}\] となるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
2° $A$ が直角のとき
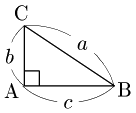
$\cos A=\cos90^\circ=0$ であるから,
\[a^2=b^2+c^2-2bc\cos90^\circ\]
すなわち
\[a^2=b^2+c^2\]
を示せばよいが,三平方の定理によりこれは成り立つ.
3° $A$ が鈍角のとき
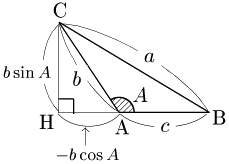
Cから辺ABの延長上に垂線CHを引く. \[\begin{align*} {\rm AH}&={\rm CA}\cos(180^\circ-A)\\[5pt] &=-{\rm CA}\cos A=-b\cos A\\[5pt] {\rm CH}&={\rm CA}\sin(180^\circ-A)\\[5pt] &=b\sin A \end{align*}\] 従って,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\]
\[\begin{align*}
\therefore a^2&=\{c+(-b\cos A)\}^2+(b\sin A)^2\\[5pt]
&=(c-b\cos A)^2+(b\sin A)^2
\end{align*}\]
この式は,$A$ が鋭角のときと同じ式 であるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
以上により,$a^2=b^2+c^2-2bc\cos A$ が示された.他の2式も同様に示される.
■
$a^2=b^2+c^2-2bc\cos A$ を示す.
$A$ が鋭角,直角,鈍角の3通りで場合分けする.
1° $A$ が鋭角のとき


Cから辺ABまたはその延長上に垂線CHを引く.$B$ が鋭角,または鈍角のときは,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\therefore a^2=|c-b\cos A|^2+(b\sin A)^2\] が成り立つ.$B$ が直角の場合は△CBHがつぶれてしまうが, $a=b\sin A$,$c=b\cos A$ であるから上の式はこの場合も含まれる.この式の右辺は \[\begin{align*} &(c^2-2bc\cos A+b^2\cos^2A)+b^2\sin^2A\\[5pt] =&b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A\\[5pt] =&b^2+c^2-2bc\cos A \end{align*}\] となるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
2° $A$ が直角のとき

$\cos A=\cos90^\circ=0$ であるから, \[a^2=b^2+c^2-2bc\cos90^\circ\] すなわち \[a^2=b^2+c^2\] を示せばよいが,三平方の定理によりこれは成り立つ.
3° $A$ が鈍角のとき

Cから辺ABの延長上に垂線CHを引く. \[\begin{align*} {\rm AH}&={\rm CA}\cos(180^\circ-A)\\[5pt] &=-{\rm CA}\cos A=-b\cos A\\[5pt] {\rm CH}&={\rm CA}\sin(180^\circ-A)\\[5pt] &=b\sin A \end{align*}\] 従って,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\begin{align*} \therefore a^2&=\{c+(-b\cos A)\}^2+(b\sin A)^2\\[5pt] &=(c-b\cos A)^2+(b\sin A)^2 \end{align*}\] この式は,$A$ が鋭角のときと同じ式 であるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
以上により,$a^2=b^2+c^2-2bc\cos A$ が示された.他の2式も同様に示される.
■

一方,これをベクトルで証明すると次のようになる.
ベクトルによる証明
証明を表示する
$a^2=b^2+c^2-2bc\cos A$ を示す.
$\overrightarrow{\rm AB}=\overrightarrow{\mathstrut b}$,$\overrightarrow{\rm AC}=\overrightarrow{\mathstrut c}$ とおくと,
\[\begin{align*}
(\mbox{左辺})&=|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut c}|^2=|\overrightarrow{\mathstrut b}|^2+|\overrightarrow{\mathstrut c}|^2-2\overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut c}\\[5pt]
&=|\overrightarrow{\mathstrut b}|^2+|\overrightarrow{\mathstrut c}|^2-2|\overrightarrow{\mathstrut b}|\,|\overrightarrow{\mathstrut c}|\cos A\\[5pt]
&=(\mbox{右辺})
\end{align*}\]
以上により,$a^2=b^2+c^2-2bc\cos A$ が示された.他の2式も同様に示される.
■
$a^2=b^2+c^2-2bc\cos A$ を示す.
$\overrightarrow{\rm AB}=\overrightarrow{\mathstrut b}$,$\overrightarrow{\rm AC}=\overrightarrow{\mathstrut c}$ とおくと,
\[\begin{align*} (\mbox{左辺})&=|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut c}|^2=|\overrightarrow{\mathstrut b}|^2+|\overrightarrow{\mathstrut c}|^2-2\overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut c}\\[5pt] &=|\overrightarrow{\mathstrut b}|^2+|\overrightarrow{\mathstrut c}|^2-2|\overrightarrow{\mathstrut b}|\,|\overrightarrow{\mathstrut c}|\cos A\\[5pt] &=(\mbox{右辺}) \end{align*}\]
以上により,$a^2=b^2+c^2-2bc\cos A$ が示された.他の2式も同様に示される.
■

ご覧のように,ベクトルだと単に式を展開しただけである!同じ定理を示すのにこれほどまでに負担が異なるのだ.このお手軽さを利用しない手はない.
●すごさその② 中線定理
中線定理と呼ばれる幾何の定理が存在する.
中線定理 △ABCにおいて,辺BCの中点をMとすると次が成り立つ.\[\rm AB^2+AC^2=2(AM^2+BM^2)\]
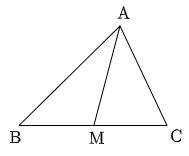
この定理を証明する方法はいくつかあり,三平方の定理を利用する方法,座標軸を設定して線分の長さを計算する方法,そしてすぐ上で述べた余弦定理を利用する方法などが考えられる.
それらによる証明方法は参考書等に譲るが,いずれもベクトルによる証明方法の簡潔さには遠く及ばない.
ベクトルによる証明
証明を表示する
$\overrightarrow{\rm AB}=\overrightarrow{\mathstrut b}$,$\overrightarrow{\rm AC}=\overrightarrow{\mathstrut c}$ とおくと,$\overrightarrow{\rm AM}=\dfrac{\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}}2$ であるから,
\[\begin{align*}
(\mbox{右辺})&=2\left(\left|\dfrac{\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}}2\right|^2+\left|\dfrac{\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b}}2\right|^2\right)\\[5pt]
&=2\left(\dfrac{|\overrightarrow{\mathstrut a}|^2+2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}+|\overrightarrow{\mathstrut b}|^2}4+\dfrac{|\overrightarrow{\mathstrut a}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}+|\overrightarrow{\mathstrut b}|^2}4\right)\\[5pt]
&=2\cdot\dfrac{2(|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2)}4\\[5pt]
&=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2\\[15pt]
&=(\mbox{左辺})
\end{align*}\]
■
$\overrightarrow{\rm AB}=\overrightarrow{\mathstrut b}$,$\overrightarrow{\rm AC}=\overrightarrow{\mathstrut c}$ とおくと,$\overrightarrow{\rm AM}=\dfrac{\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}}2$ であるから,
\[\begin{align*} (\mbox{右辺})&=2\left(\left|\dfrac{\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}}2\right|^2+\left|\dfrac{\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b}}2\right|^2\right)\\[5pt] &=2\left(\dfrac{|\overrightarrow{\mathstrut a}|^2+2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}+|\overrightarrow{\mathstrut b}|^2}4+\dfrac{|\overrightarrow{\mathstrut a}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}+|\overrightarrow{\mathstrut b}|^2}4\right)\\[5pt] &=2\cdot\dfrac{2(|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2)}4\\[5pt] &=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2\\[15pt] &=(\mbox{左辺}) \end{align*}\]
■


このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |