高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

6.ベクトル方程式
等式には方程式と恒等式があって,方程式とは特定の値でのみ成立する等式,恒等式とはいかなる値でも成立する等式である.方程式の例としては
6.1 直線のベクトル方程式
直線のベクトル方程式は,ちょっとした思考の転換が必要
これからベクトルによって直線を表そうという訳だが,これまでの
という流れであり,従って方程式の左辺は「
といったように,
このように,ベクトルで直線を表現するには従来とやや異なった思考が必要である.
ではどのようにベクトルで直線を表現するのか
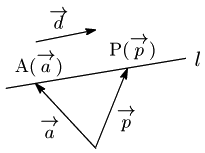
直線
であるから,
点Pが
が成り立つ.
直線のベクトル方程式点

変化させたときの,点Pの動き方
補足
見た目が異なるので直線に見えない…でも中身は同じ
私たちは
1つだけ例を挙げると,直線
と表せる.逆に,
①×3-②×2 から
となって元の方程式が得られる.
注意
方向ベクトルは実数倍の任意性がある
すぐ上で上げた例では方向ベクトルとして
など方向ベクトルはただ1つには定まらず,実数倍されたもの(ただし0倍は除く)はどれでもその直線の方向ベクトルとして採用してよい.
例題 点(2,1)を通り,
このとき
よって,直線は
補足
①の2式より

6.2 2点を通る直線のベクトル方程式
通る2点がわかれば直線は決定する
数学Ⅱの図形と方程式 では,直線が通る2点
という具合に方程式を導くことができた.ベクトルでも直線上の2点を表す位置ベクトルがわかれば方程式を導くことができる.
2点
まとめ 2点A
補足
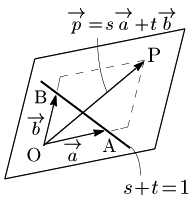
定理

6.3 法線ベクトルと直線
直線に垂直なベクトルを用いた直線の表現
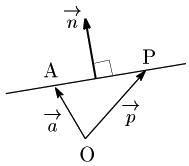
点
このとき,
により,
これを,点A
まとめ 点A
この表現では媒介変数が必要ない
最初に出てきた直線のベクトル方程式は
というようにベクトルの平行条件を元にして導いたのに対して,後者は
というようにベクトルの垂直条件を元にして導いたためである.
この表現も
上の式が直線を表していることを確かめてみよう.
逆に直線
直線の法線ベクトル 直線
注意
方向ベクトルと同様に,法線ベクトルも実数倍の任意性がある.
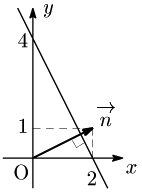
例
直線

6.4 円のベクトル方程式
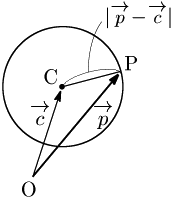
中心
円のベクトル方程式
点
円の方程式でも双方向に変換が可能
上の式から,数学Ⅱの円の方程式 で学んだ
この計算の逆をたどれば,円のベクトル方程式が得られる.
2点を直径の両端とする円
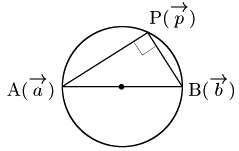
2点
であるから,
2点
この式が円を表すことを確かめよう.
中心の位置ベクトル
半径
よって,
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | |||
| 2. ベクトルの演算 | |||
| 3. ベクトルの成分 | |||
| 4. ベクトルの内積 | |||
| 5. 位置ベクトル | |||
| 6. ベクトル方程式 | |||
| 7. 平面ベクトルの応用 | |||
| 8. 空間ベクトル | |||
| 9. 空間ベクトルの成分 | |||
| 10. 空間ベクトルの内積 | |||
| 11. 空間の位置ベクトル | |||
| 12. 空間ベクトルの応用 | |||
| 13. 空間のベクトル方程式 |

