高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | |||
| 2. メネラウスの定理 | |||
| 3. チェバの定理の逆 | |||
| 4. メネラウスの定理の逆 | |||
| 5. 円に内接する四角形 | |||
| 6. 接弦定理とその逆 | |||
| 7. 方べきの定理とその逆 | |||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | |||
| 2. 円周角の定理の逆 |

1.円の内部・外部
ある点Pと,△ABCの外接円Cがあるとする.点Pと円Cの位置関係は,
1° 円の内部 2° 円の外部 3° 円周上
のいずれかであってこれ以外にない.この3つのうちのどれであるかは角の大小関係によって判定できる.
2点C,Pが直線ABについて同じ側にあるとする.
図において,弧ABに対する円周角ACBと∠APBについて,
[1] 点Pが円の内部
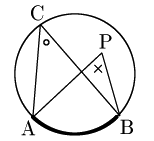
[2] 点Pが円の外部
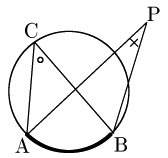
証明の方針
まず「
証明
まず「
[1] 点Pが円の内部
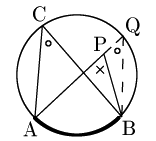
図のように半直線APと円との交点をQとする.△BPQの内角と外角の関係により
[2] 点Pが円の外部
1° 半直線APまたはBPが円と交わるとき
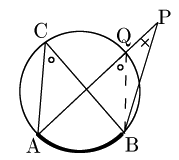
図のようにAPと円との交点をQとする.△BPQの内角と外角の関係により
2° 半直線APもBPも円と交わらないとき
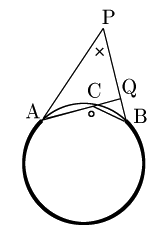
図のように半直線ACとBPの交点をQとすると,三角形の内角と外角の関係により
よって「
次に「
[1] 点Pが円の内部
点Pは円の内部にあるか,外部にあるか,円周上にあるかのいずれかである.
また,点Pが円周上にあるとすれば,円周角の定理により
従って点Pは円の内部にある.
[2] 点Pが円の外部
点Pは円の内部にあるか,外部にあるか,円周上にあるかのいずれかである.
また,点Pが円周上にあるとすれば,円周角の定理により
従って点Pは円の内部にある.
よって「
以上により「
■

2.円周角の定理の逆
先に議論した円の内部・外部の関係から,次の「円周角の定理の逆」が成り立つ:
2点C,Pが直線ABについて同じ側にあるとする.このとき,∠ACB
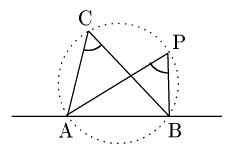
証明
点Pは△ABCの外接円の周上にあるか,そうでないかのいずれかであるが,上の定理により,
であるから,∠ACB
■
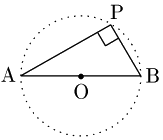
補足
線分ABを直径とする円周上に点Cをとって三角形ABCを作ると,

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | |||
| 2. メネラウスの定理 | |||
| 3. チェバの定理の逆 | |||
| 4. メネラウスの定理の逆 | |||
| 5. 円に内接する四角形 | |||
| 6. 接弦定理とその逆 | |||
| 7. 方べきの定理とその逆 | |||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | |||
| 2. 円周角の定理の逆 |
