数学A 第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
演習問題
問題１ [難易度 易]
△ABCにおいて，辺ABを $2:1$ に内分する点をD，辺ACを $2:3$ に内分する点をEとし，BE，CDの交点をPとする．直線APと辺BCとの交点をQとするとき，$\rm{BQ:QC}$ を求めよ．
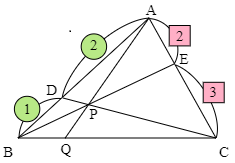
問題２ [難易度 標準]
△ABCにおいて，辺ABを $3:1$ に外分する点をD，辺ACを $5:2$ に外分する点をEとし，BE，CDの交点をPとする．直線APとBCとの交点をQとするとき，$\rm{BQ:QC}$ を求めよ．
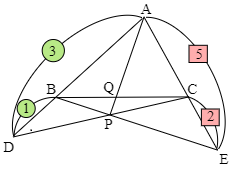
問題３ [難易度 標準]
△ABCにおいて，辺AB上を $2:1$ に内分する点をDとし，Dを通ってBCに平行な直線とACとの交点をEとする．BE，CDの交点をPとし，直線APとBCとの交点をQとするとき，QはBCの中点であることを示せ．
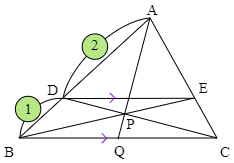
チェバの定理の式は辺の長さを用いた式になっていますが，例えば $\rm{\dfrac{BQ}{QC}}$ という部分は $\rm{BQ:QC}$ の比の値です．従って辺の長さそのものがわからなくても，比の値さえわかればよいという訳です． POINT
問題１【基本】
△ABCにおいて，辺ABを $2:1$ に内分する点をD，辺ACを $2:3$ に内分する点をEとし，BE，CDの交点をPとする．直線APとBCとの交点をQとするとき，$\rm{BQ:QC}$ を求めよ．
解答
チェバの定理により \[\rm{\frac{BQ}{QC}\cdot\frac{CE}{EA}\cdot\frac{AD}{DB}}=1\] よって \[\rm{\frac{BQ}{QC}\cdot\frac32\cdot\frac21=1}\] 従って $\rm{\dfrac{BQ}{QC}}=\dfrac13$
故に $\rm{BQ}:{QC}=1:3$
補足
チェバの定理は，点が三角形の内部にある場合と外部にある場合の2パターンがありますが，いずれもある頂点からスタートして3ステップで元の頂点に戻ってくるように比の式を作ればよい訳です．本問は点Pが△ABCの内部にあり，この場合が使えるようになっておけば大抵の場合用が足ります．3つのステップ全てが内分であるケースです．
問題２【標準】
△ABCにおいて，辺ABを $3:1$ に外分する点をD，辺ACを $5:2$ に外分する点をEとし，BE，CDの交点をPとする．直線APとBCとの交点をQとするとき，$\rm{BQ:QC}$ を求めよ．