円に内接する四角形-対角の和が180°・4点が同一円周上などスライドでわかりやすく解説

このページにある内容は，こちらのスライド(会員向け) でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

中学校の範囲

5．円に内接する四角形

1．四角形の対角の和

　三角形には外接円が必ず存在する(外心 参照)．しかし，ここにもう1点――思いつきで適当に――追加し，三角形の3頂点と合わせた4つの点を考えるとき，もはやその4点が1つの円周上にあることは全く保証されない．三角形が確実に円に内接できるのに対して，四角形は円に内接できるかどうかは4番目の点の配置次第である．その理由は，三角形を決めると，それに応じて外接円がたった1つ決まるが，四角形では残りの1点がこの外接円上に制限されず，どこにでも存在する可能性があるからだ．

　以下で四角形が円に内接するための条件，換言すると4点が同一円周上にあるための条件を確認していくのであるが，四角形が円に内接する条件はこれ以外にもいくつかの言い換えがある．それらの筆頭ともいえるほど重要なのが，次の定理である．四角形が円に内接するかどうかの判定は，共通テスト等でも問われる可能性が大いにある．定理の内容が理解出来たら演習問題 で実践トレーニングを行っておこう．

定理

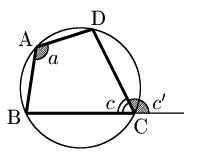
四角形が円に内接する　　　　　　　
$\iff$ 対角の和が180°　$(a\!+\!c\!=\!180^\circ)$　　　　
$\iff$ 内角が，その対角の外角に等しい ($a\!=\!c’$)

証明の方針

• 「四角形が円に内接する $\Rightarrow$ 対角の和が180°」は，円周角の定理 を利用．
• 「四角形が円に内接する $\Leftarrow$ 対角の和が180°」は，△ABDの外接円上点${\rm C}\,’$ をとり，円周角の定理の逆 を利用．
• 「対角の和が180°$\iff$内角が，その対角の外角に等しい」は明らか．

証明

「四角形が円に内接する $\Rightarrow$ 対角の和が180°」を示す．

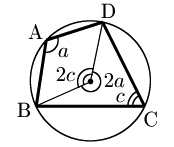
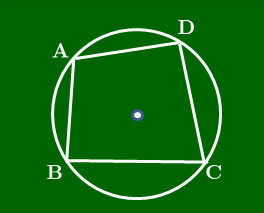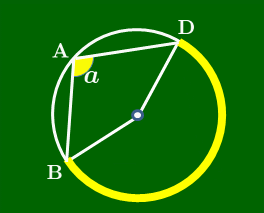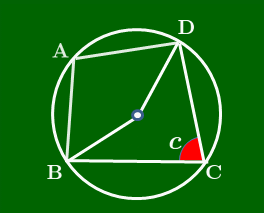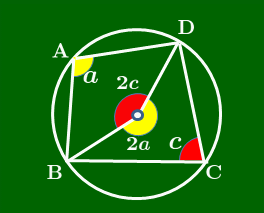
　円周角の定理 により図のようになるから，中心角に注目すると， \[2a+2c=360^\circ\] \[\therefore a+c=180^\circ\]

「四角形が円に内接する $\Leftarrow$ 対角の和が180°」を示す．