三角形の五心 – 外心(ノート)

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

	スライド	ノート	問題
1. チェバの定理	[無料]		[会員]
2. メネラウスの定理	[無料]		[会員]
3. チェバの定理の逆	[無料]
4. メネラウスの定理の逆	[会員]
5. 円に内接する四角形	[会員]		[会員]
6. 接弦定理とその逆	[会員]
7. 方べきの定理とその逆	[会員]
8. 三角形の五心
重心
外心
垂心
内心
傍心

---

中学校の範囲

	スライド	ノート	問題
1. 円周角の定理			[会員]
2. 円周角の定理の逆			[会員]

外心

　ここでの目標は，三角形に外心と呼ばれる点が存在することを示すことにある．

1．円と弦

まずは準備として，円の中心と弦の関係を確認

定理
[1]　円の中心Oから弦ABに引いた垂線は，その弦を2等分する．

[2]　円の中心Oは弦ABの垂直二等分線上にある．

証明

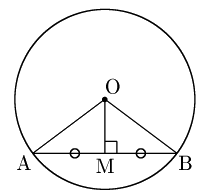
　中心Oから弦ABに垂線OMを下ろす．

[1]　円の中心Oから弦ABに引いた垂線は，その弦を2等分する．

　△OAMと△OBMにおいて，仮定より

$\angle\rm OMA=\angle OMB=90^\circ\ \cdots$ ①

　OAとOBは円の半径だから

$\rm OA=OB\ \cdots$ ②

　また，

$\rm OM$ は共通 $\cdots$ ③

　①～③より直角三角形の斜辺と他の1辺がそれぞれ等しいから △OAM≡△OBM．故に $${\rm AM}={\rm BM}$$

[2]　円の中心Oは弦ABの垂直二等分線上にある．

　上の基本事項の確認から，弦ABの両端から等しい距離にある点はすべて弦ABの垂直二等分線上にある．このことは中心Oも弦ABの垂直二等分線上にあることを意味する．

■

2．外心

三角形の外心とは

　前節の準備の下，外心について説明をする．

定理
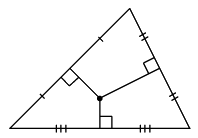
　三角形の3辺の垂直二等分線は1点で交わる．

証明

辺ABとACの垂直二等分線の交点をOとする．

上の基本事項の確認により $$\left\{\begin{array}{l} {\rm OA}={\rm OB}\\[5pt] {\rm OA}={\rm OC} \end{array}\right.$$ であるから， $${\rm OB}={\rm OC}$$ が成り立つ：

　よって，上の基本事項の確認により，点Oは辺BCの垂直二等分線上にもあるから，3本の垂直二等分線は1点Oで交わることが示された．

■

補足

　定理の証明過程から，どんな三角形にも3つの頂点を通る円がただ1つ存在することがわかる．何故なら2本の辺の垂直二等分線は平行でないため，交点が必ず存在するからである．3頂点を通る円をその三角形の外接円といい，外接円の中心を外心という．

3．外心・外接円の作図

外心・外接円を定規とコンパスで作図する方法

　三角形の3本の辺のうちの2本を選んで，それぞれの垂直二等分線を描く．その交点が外心．外心を中心として各頂点を通る円を描けば，外接円となる．

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

中学校の範囲